文章来源:初识 CV - Transformer 模型详解(图解最完整版)
T r a n s f o r m e r Transformer T r a n s f o r m e r 2017 2017 2 0 1 7 关注重点、忽略无关内容
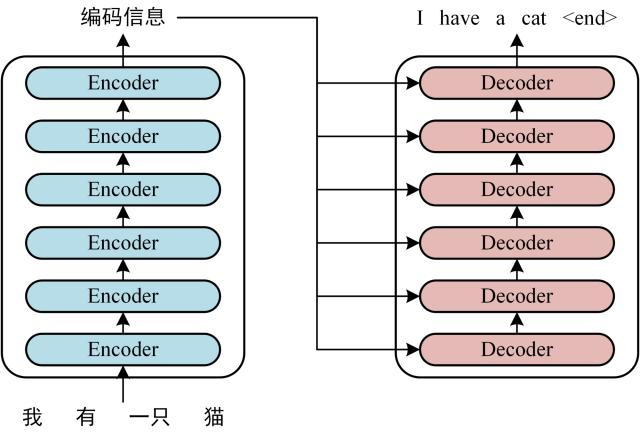
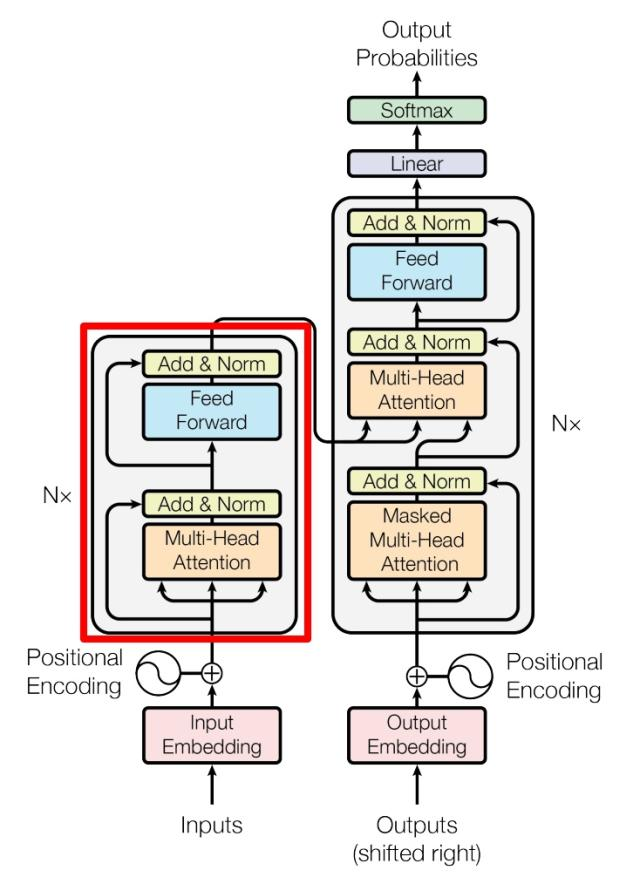
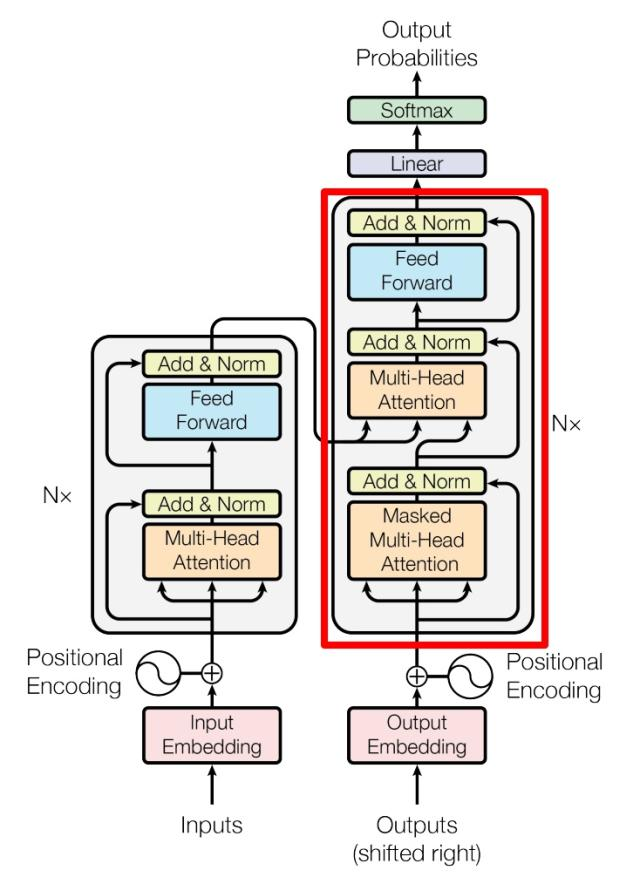
# 结构T r a n s f o r m e r Transformer T r a n s f o r m e r E n c o d e r Encoder E n c o d e r D e c o d e r Decoder D e c o d e r
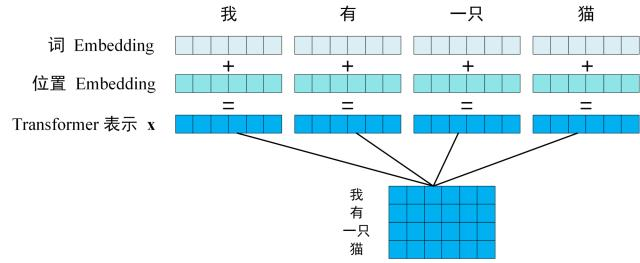
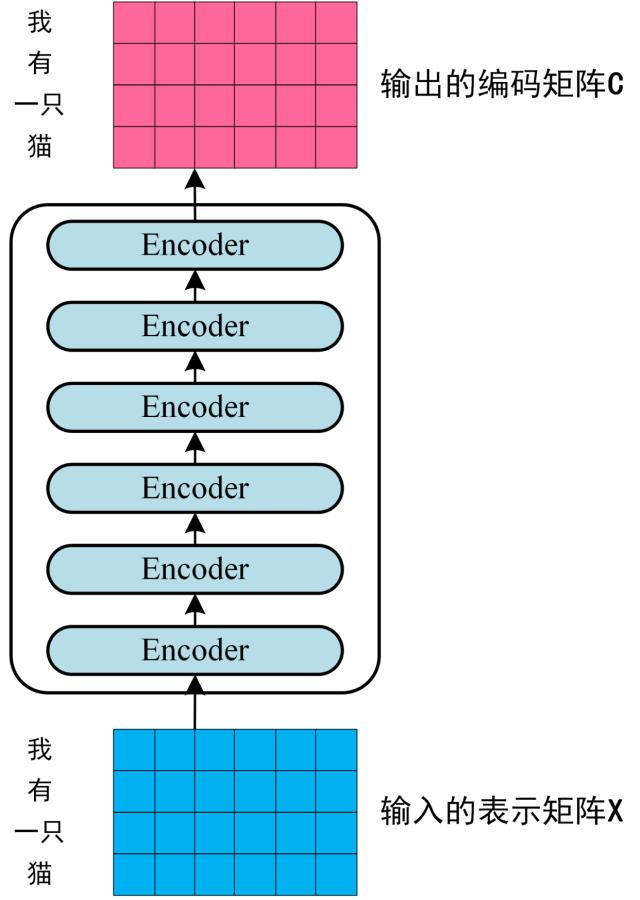
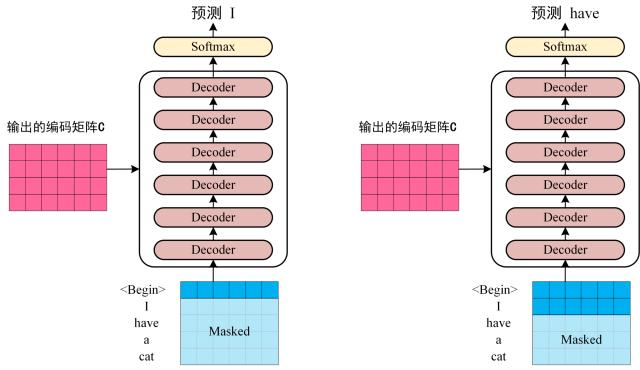
# 工作流程获取输入句子的每一个表示向量 x x x 单词的意思Embedding 和 单词的位置Embedding 相加得到 将得到的 表示向量矩阵 (每一行是一个 表示向量 ),传入 E n c o d e r Encoder E n c o d e r 6 6 6 E n c o d e r Encoder E n c o d e r C C C 将编码矩阵 C C C D e c o d e r Decoder D e c o d e r D e c o d e r Decoder D e c o d e r 1 → i − 1 1 \to i - 1 1 → i − 1 i i i Mask(掩盖) 操作遮盖住 i + 1 i + 1 i + 1 # 单词的词意 Embedding可以通过 W o r d 2 V e c Word2Vec W o r d 2 V e c G l o v e Glove G l o v e T r a n s f o r m e r Transformer T r a n s f o r m e r
# 单词的位置 EmbeddingT r a n s f o r m e r Transformer T r a n s f o r m e r 自注意力机制 ,把句子中的所有词当成一个集合,但有个问题是 我 爱 你 和 你 爱 我 ,他们会是一样的集合,丢失顺序信息,而此时,我们就提出了位置 E m b e d d i n g Embedding E m b e d d i n g
假设一句话有 L L L d m d_{m} d m p o s pos p o s P o s i t i o n a l E n c o d i n g ( P E ) Positional~Encoding~(PE) P o s i t i o n a l E n c o d i n g ( P E ) d m d_m d m E m b e d d i n g Embedding E m b e d d i n g E m b e d d i n g Embedding E m b e d d i n g
# 公式P E ( p o s , 2 i ) = s i n ( p o s 1000 0 2 i / d m ) PE(pos, 2i) = sin(\frac{pos}{10000^{2i / d_{m}}}) P E ( p o s , 2 i ) = s i n ( 1 0 0 0 0 2 i / d m p o s )
P E ( p o s , 2 i + 1 ) = c o s ( p o s 1000 0 2 i / d m ) PE(pos, 2i+1)=cos(\frac{pos}{10000^{2i/d_m}}) P E ( p o s , 2 i + 1 ) = c o s ( 1 0 0 0 0 2 i / d m p o s )
以 我 爱 你 为例
位置 p o s = 0 , 1 , 2 pos = 0, 1, 2 p o s = 0 , 1 , 2 d m d_{m} d m 4 4 4 i = 0 , 1 , 2 , 3 i = 0, 1, 2, 3 i = 0 , 1 , 2 , 3 每一个词都可以代入,得到一个唯一的位置 E m b e d d i n g Embedding E m b e d d i n g
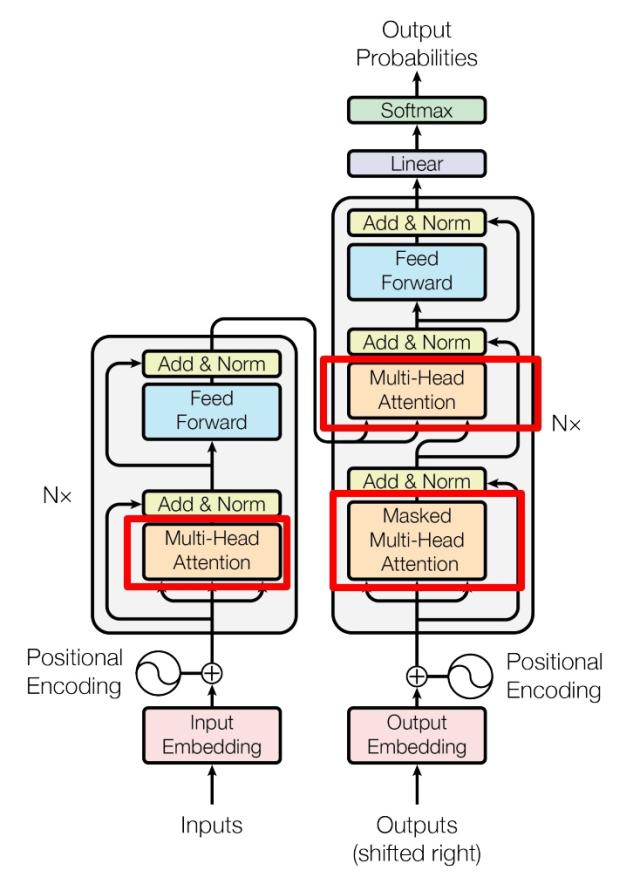
# Self-Attention(自注意机制)M u l t i − H e a d A t t e n t i o n Multi-Head~Attention M u l t i − H e a d A t t e n t i o n S e l f − A t t e n t i o n Self-Attention S e l f − A t t e n t i o n E n c o d e r Encoder E n c o d e r M u l t i − H e a d A t t e n t i o n Multi-Head~Attention M u l t i − H e a d A t t e n t i o n D e c o d e r Decoder D e c o d e r M u l t i − H e a d A t t e n t i o n Multi-Head~Attention M u l t i − H e a d A t t e n t i o n
每个 M u l t i − H e a d A t t e n t i o n Multi-Head~Attention M u l t i − H e a d A t t e n t i o n A d d & N o r m Add ~ \& ~ Norm A d d & N o r m
A d d Add A d d R e s i d u a l C o n n e c t i o n Residual~Connection R e s i d u a l C o n n e c t i o n N o r m Norm N o r m L a y e r N o r m a l i z a t i o n Layer~Normalization L a y e r N o r m a l i z a t i o n # Self-Attention 结构S e l f − A t t e n t i o n Self-Attention S e l f − A t t e n t i o n x x x x x x E n c o d e r Encoder E n c o d e r
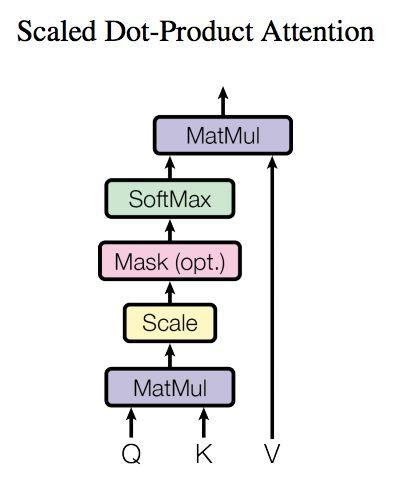
Q , K , V Q,K,V Q , K , V
Q ( Q u e r y ) Q~(Query) Q ( Q u e r y ) K ( K e y ) K~(Key) K ( K e y ) V ( V a l u e ) V~(Value) V ( V a l u e ) 在数学形式上,就是三个线性变换
Q = X ⋅ W Q , K = X ⋅ W K , V = X ⋅ W V Q = X·W_Q, K = X·W_K,V=X·W_V Q = X ⋅ W Q , K = X ⋅ W K , V = X ⋅ W V
W Q , K , V ∈ R d m × d k W_{Q,K,V} \in \mathbb{R}^{d_{m} \times d_k} W Q , K , V ∈ R d m × d k d k d_k d k d m d_m d m 用 Q Q Q K K K
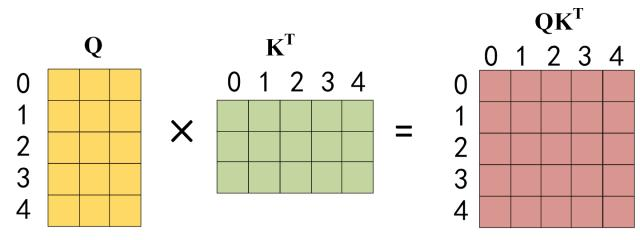
S c o r e s = Q ⋅ K T ∈ R n × n Scores = Q·K^{T} \in \mathbb{R}^{n \times n} S c o r e s = Q ⋅ K T ∈ R n × n
这样一个 n × n n \times n n × n i i i j j j d k \sqrt{d_k} d k
S c o r e s c a l e d = Q ⋅ K T d k Score_{scaled}=\frac{Q·K^T}{\sqrt{d_k}} S c o r e s c a l e d = d k Q ⋅ K T
再对每一行做 S o f t M a x SoftMax S o f t M a x
A t t e n t i o n W e i g h t s = S o f t M a x ( Q ⋅ K T d k ) Attention~Weights = SoftMax(\frac{Q·K^T}{\sqrt{d_k}}) A t t e n t i o n W e i g h t s = S o f t M a x ( d k Q ⋅ K T )
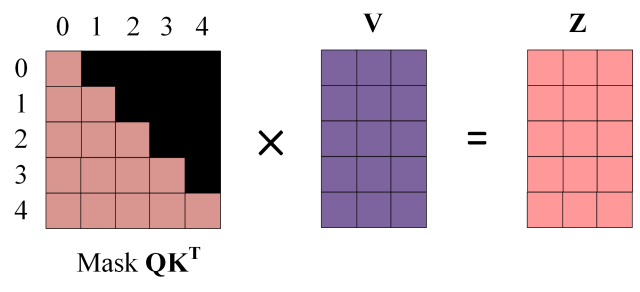
用这样的权重去加和 V V V
O u t p u t = V ⋅ A t t e n t i o n W e i g h t s ∈ R n × d v Output = V·Attention~Weights \in \mathbb{R}^{n \times d_v} O u t p u t = V ⋅ A t t e n t i o n W e i g h t s ∈ R n × d v
通过这样的形式,就能更新每个词的表示,同时还能融合其他词的信息
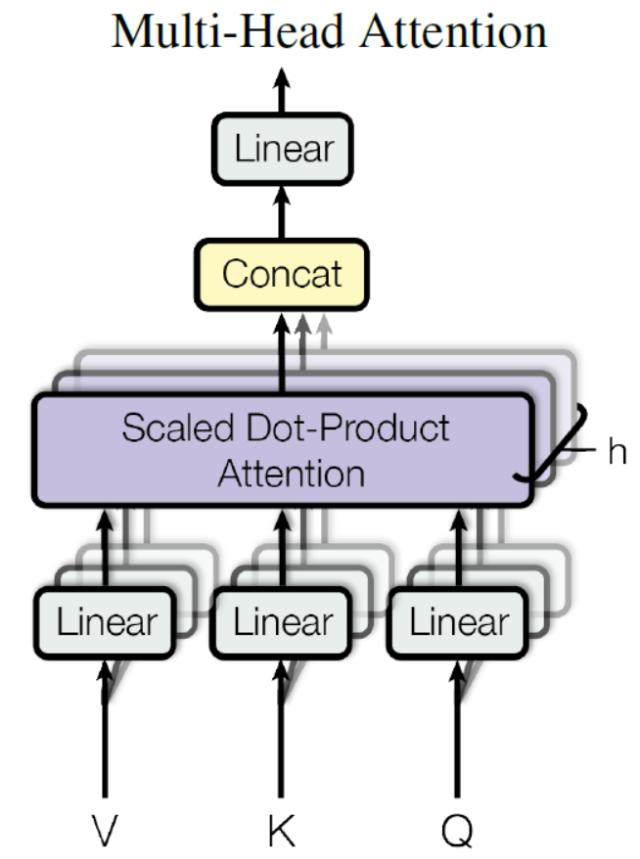
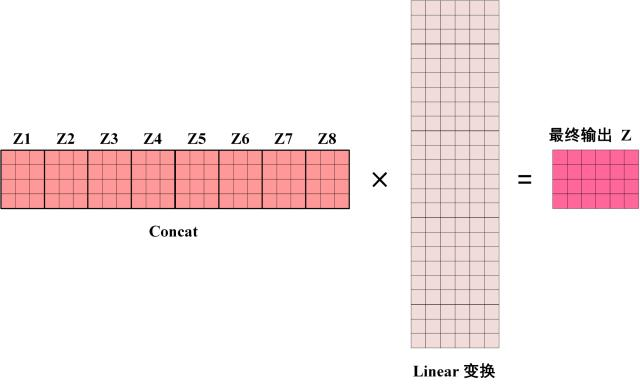
# Multi-Head Attention(多头注意力机制)M u l t i − H e a d A t t e n t i o n Multi-Head~Attention M u l t i − H e a d A t t e n t i o n S e l f − A t t e n t i o n Self-Attention S e l f − A t t e n t i o n x x x h h h S e l f − A t t e n t i o n Self-Attention S e l f − A t t e n t i o n h h h Z Z Z h h h Z Z Z C o n c a t Concat C o n c a t L i n e a r Linear L i n e a r M u l t i − H e a d A t t e n t i o n Multi-Head~Attention M u l t i − H e a d A t t e n t i o n
# Encoder 结构E n c o d e r Encoder E n c o d e r Add & Norm 和 Feed Forward 部分,这里进行一个补充介绍
# Add & NormO u t p u t = L a y e r N o r m ( x + S u b L a y e r ( x ) ) Output = LayerNorm(x+SubLayer(x)) O u t p u t = L a y e r N o r m ( x + S u b L a y e r ( x ) )
顾名思义,这个部分分为
A d d Add A d d N o r m Norm N o r m # Add计算完上一层的输入 S u b L a y e r ( x ) SubLayer(x) S u b L a y e r ( x )
y = x + S u b L a y e r ( x ) y = x + SubLayer(x) y = x + S u b L a y e r ( x )
通过相加,既能保留原始信息,又能叠加上新信息,缓解梯度消失的问题
# Norm对 A d d Add A d d y y y L a y e r N o r m a l i z a t i o n Layer~Normalization L a y e r N o r m a l i z a t i o n
L a y e r N o r m ( y ) = γ ⋅ y − μ σ 2 + ϵ + β LayerNorm(y) = \gamma· \frac{y - \mu}{\sqrt{\sigma^2+\epsilon}} + \beta L a y e r N o r m ( y ) = γ ⋅ σ 2 + ϵ y − μ + β
μ = 1 d ∑ i = 1 d y i \mu = \frac{1}{d} \sum\limits_{i=1}^{d} y_i μ = d 1 i = 1 ∑ d y i σ 2 \sigma^2 σ 2 d d d γ , β \gamma,\beta γ , β ϵ \epsilon ϵ 0 0 0 # Feed Forward(前馈全连接网络 FFN)F F N FFN F F N 两层全连接 + 激活函数
F F N ( x ) = W 2 ⋅ σ ( W 1 ⋅ x + b 1 ) + b 2 FFN(x) = W_2 · \sigma(W_1·x+b_1)+b_2 F F N ( x ) = W 2 ⋅ σ ( W 1 ⋅ x + b 1 ) + b 2
W 1 ∈ R d f × d m W_1 \in \mathbb{R}^{d_f \times d_m} W 1 ∈ R d f × d m d m d_m d m b 1 ∈ R d f b_1 \in \mathbb{R}^{d_f} b 1 ∈ R d f σ ( ⋅ ) \sigma(·) σ ( ⋅ ) R e L U ReLU R e L U G E L U GELU G E L U W 2 ∈ d m × d f W_2 \in \mathbb{d_m \times d_f} W 2 ∈ d m × d f d m d_m d m b 2 ∈ R d m b_2 \in \mathbb{R}^{d_m} b 2 ∈ R d m 通俗易懂的解释就是,一句话的表达 x x x
# Decoder 结构
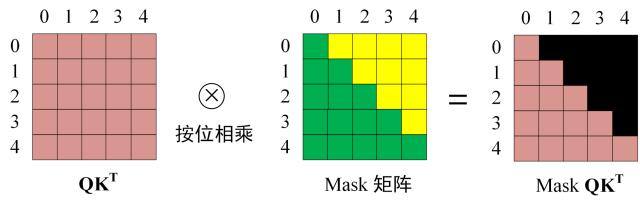
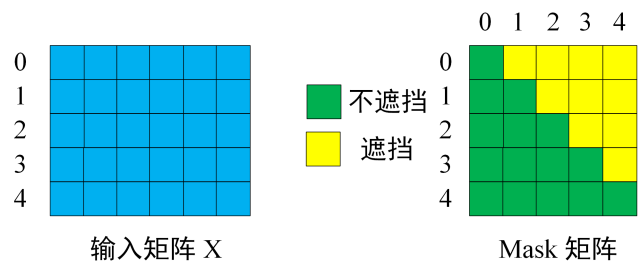
# 第一个 MHAD e c o d e r Decoder D e c o d e r M H A MHA M H A M a s k e d Masked M a s k e d i i i i + 1 i+1 i + 1 注意 ,M a s k e d Masked M a s k e d S e l f − A t t e n t i o n Self-Attention S e l f − A t t e n t i o n S o f t m a x Softmax S o f t m a x M a s k e d Masked M a s k e d
第一步仍是 Q ⋅ K T Q · K^T Q ⋅ K T Q K T QK^T Q K T 区别就是,要在 S o f t m a x Softmax S o f t m a x M a s k e d Masked M a s k e d 用 M a s k ( Q ⋅ K T ) Mask(Q·K^T) M a s k ( Q ⋅ K T ) # 第二个 MHA第二个 M u l t i − H e a d A t t e n t i o n Multi-Head~Attention M u l t i − H e a d A t t e n t i o n M H A MHA M H A S e l f − A t t e n t i o n Self-Attention S e l f − A t t e n t i o n K , V K, V K , V Encoder 的编码信息矩阵 C 计算的,而不是使用上一个 D e c o d e r Decoder D e c o d e r
K , V K, V K , V E n c o d e r Encoder E n c o d e r C C C Q Q Q D e c o d e r Decoder D e c o d e r 这样的好处是,在 D e c o d e r Decoder D e c o d e r E n c o d e r Encoder E n c o d e r M a s k e d Masked M a s k e d
# Softmax其实是得到一堆 S o f t m a x Softmax S o f t m a x
![]()
![]()
![]()
![]()
![]()
![]()