# KMP 算法的定义K M P KMP K M P S S S P P P
假设现在文本串 S S S i i i j j j
如果 j = -1 ,或者当前字符匹配成功( s[i] == p[j] ),都令 i++, j++ ,然后继续匹配下一个字符 如果 j != -1 ,并且当前字符匹配失败( s[i] != p[j] ),则令 i i i j = next[j] 。此操作意味着当匹配失败时,模式串 P P P S S S j - next[j] 位 # next 数组的含义表示当前字符之前的字符串中,有多大长度的相同前后缀。例如如果 next[j] = k ,则代表 j j j k k k n e x t next n e x t next[j] 的位置)next[j] 等于 0 0 0 − 1 -1 − 1 next[j] = k 且 k > 0 ,则代表下次匹配跳到 j j j k k k
# KMP 算法的步骤# 寻找前缀后缀最长公共元素长度对于 p = p0 p1 ... pj-1 pj ,寻找模式串 P P P P 0 , P 1 , . . . , P k − 1 = P j − k , = P j − k , P j − k + 1 , . . . , P j P_0,~P_1,~...,~P_{k-1}~=~P_{j-k},~=P_{j-k},~P_{j-k+1},~...,~P_j P 0 , P 1 , . . . , P k − 1 = P j − k , = P j − k , P j − k + 1 , . . . , P j P j P_j P j k + 1 k+1 k + 1 P P P a b a b abab a b a b
模式串 a a a b b b a a a b b b 最大前缀后缀公共元素长度 0 0 0 0 0 0 1 1 1 2 2 2
# 求 next 数组n e x t next n e x t 除当前字符外的最长相同前后缀串长度 ,所以求得各个前缀后缀的公共元素最大长度后,只要稍作变形即可,将步骤一中求得的值整体右移一位,初始值赋为 − 1 -1 − 1
模式串 a a a b b b a a a b b b n e x t next n e x t − 1 -1 − 1 0 0 0 0 0 0 1 1 1
next[i] 表示第 i i i next[i] 的相同前缀后缀字符串
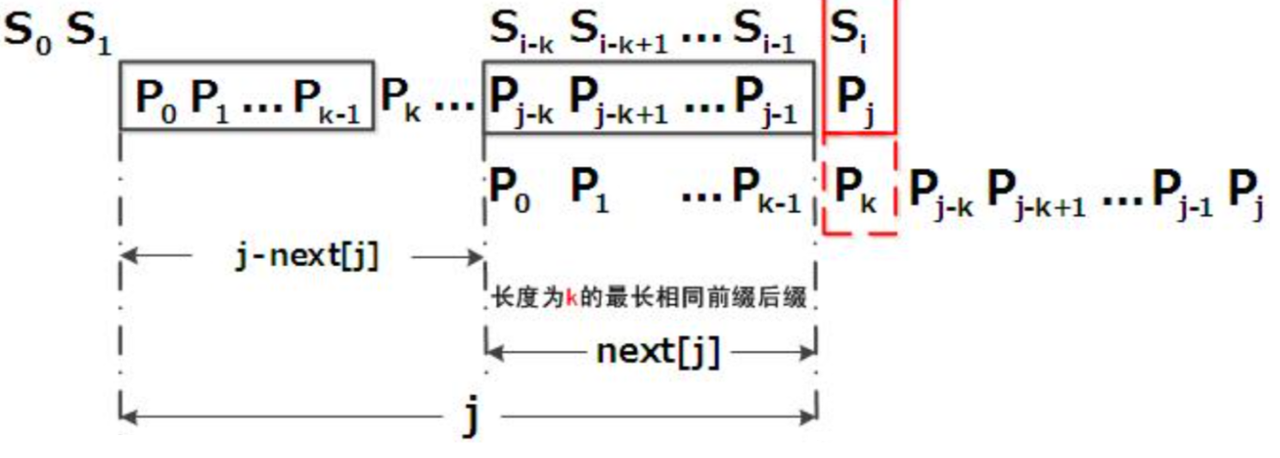
# 根据 n e x t next n e x t 如果匹配失败,模式串向右移动的位数为: j - next[j]P j − k , P j − k + 1 , . . . , P j − 1 P_{j-k},~P_{j-k+1},~...,~P_{j-1} P j − k , P j − k + 1 , . . . , P j − 1 S i − k , S i − k + 1 , . . . , S i − 1 S_{i-k},~S_{i-k+1},~...,~S_{i-1} S i − k , S i − k + 1 , . . . , S i − 1 P j P_j P j S i S_i S i next[j] = k ,相当于在不包含 P j P_j P j k k k P 0 , P 1 , . . . , P k − 1 = P j − k , = P j − k , P j − k + 1 , . . . , P j P_0,~P_1,~...,~P_{k-1}~=~P_{j-k},~=P_{j-k},~P_{j-k+1},~...,~P_j P 0 , P 1 , . . . , P k − 1 = P j − k , = P j − k , P j − k + 1 , . . . , P j j = next[j] ,从而让模式串右移 j - next[j] 位,使得模式串的前缀 P 0 , P 1 , . . . , P k − 1 P_0,P_1,~...,~P_{k-1} P 0 , P 1 , . . . , P k − 1 S i − k , S i − k + 1 , . . . , S i − 1 S_{i-k},~S_{i-k+1},~...,~S_{i-1} S i − k , S i − k + 1 , . . . , S i − 1 P k P_k P k S i S_i S i
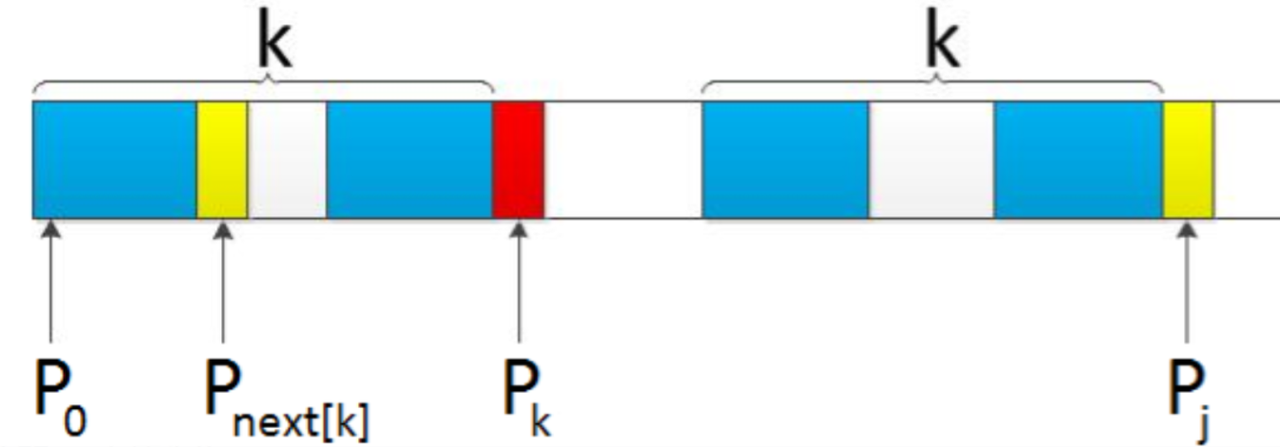
# 递推计算 next 数组# 再次介绍 next 数组的含义如果对于 k k k P 0 , P 1 , P k − 1 = P j − k , P j − k + 1 , . . . , P j − 1 P_0,~P_1,~P_{k-1}~=~P_{j-k},~P_{j-k+1},~...,~P_{j-1} P 0 , P 1 , P k − 1 = P j − k , P j − k + 1 , . . . , P j − 1 next[j] = k 。next[j] = k 代表 P 0 → P j − 1 P_0~\to~P_{j-1} P 0 → P j − 1 k k k n e x t next n e x t j j j n e x t [ j ] next[j] n e x t [ j ] j - next[j] 位
已知 n e x t [ 0 , . . . , j ] next[0,~...,~j] n e x t [ 0 , . . . , j ] n e x t [ j + 1 ] next[j~+~1] n e x t [ j + 1 ] 对于 P P P j + 1 j+1 j + 1 如果 p[k] == p[j] ,则 next[j + 1] = next[j] + 1 = k + 1 。 如果 p[k] != p[j] ,如果此时的 p[next[k]] == p[j] ,则 next[j + 1 = next[k] + 1 ,否则继续递归前缀索引 k = next[k] ,而后重复此过程。相当于在字符 P j + 1 P_{j+1} P j + 1 k + 1 k+1 k + 1 P 0 , P 1 , . . . , P k P_0,~P_1,~...,~P_k P 0 , P 1 , . . . , P k P j − k , P j − k + 1 , . . . , P j − 1 , P j P_{j-k},~P_{j-k+1},~...,~P_{j-1},~P_j P j − k , P j − k + 1 , . . . , P j − 1 , P j t + 1 ≤ k + 1 t+1~\le~k+1 t + 1 ≤ k + 1 P 0 , P 1 , . . . , P t − 1 , P t P_0,~P_1,~...,~P_{t-1},~P_t P 0 , P 1 , . . . , P t − 1 , P t P j − 1 , P j − t + 1 , . . . , P j − 1 , P j P_{j-1},~P_{j-t+1},~...,~P_{j-1},~P_j P j − 1 , P j − t + 1 , . . . , P j − 1 , P j t + 1 t+1 t + 1 n e x t [ j + 1 ] next[j+1] n e x t [ j + 1 ] n e x t next n e x t n e x t [ 0 , . . . , k , . . . , j ] next[0,~...,~k,~...,~j] n e x t [ 0 , . . . , k , . . . , j ] P P P P P P # 如何理解上面这个抽象的描述情况 1: P k = P j P_k~=~P_j~ P k = P j 模式串 A \color{red}A A B \color{red}B B C \color{green}C C D D D A \color{red}A A B \color{red}B B C \color{green}C C E E E 相同前后缀长度 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 2 2 2 3 3 3 0 0 0 n e x t next n e x t − 1 -1 − 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 2 2 2 ? ? ? 索引 P 0 P_0 P 0 P_ P k P_k P k P_ P_ P_ P j P_j P j P_
因为 P k = P j = ′ C ′ P_k~=~P_j~=~'C' P k = P j = ′ C ′ next[j + 1] = next[j] + 1 = k + 1 (可以看出 next[j + 1] = 3 )E E E k + 1 k+1 k + 1
情况 2: P k ≠ P j P_k~\not=~P_j P k = P j 模式串 A \color{red}A A B \color{red}B B C \color{green}C C D D D A \color{red}A A B \color{red}B B D \color{blue}D D E E E 相同前后缀长度 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 2 2 2 0 0 0 0 0 0 n e x t next n e x t − 1 -1 − 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 2 2 2 ? ? ? 索引 P 0 P_0 P 0 P_ P k \color{green}P_k P k P_ P_ P_ P j \color{blue}P_j P j
P k ≠ P j P_k~\not=~P_j P k = P j P 0 , P k − 1 , P k ≠ P j − k , P j − 1 , P j P_0,~P_{k-1},~P_k~\not=~P_{j-k},~P_{j-1},~P_j P 0 , P k − 1 , P k = P j − k , P j − 1 , P j E E E ′ C ′ ≠ ′ D ′ 'C'~\not=~'D' ′ C ′ = ′ D ′ E E E k + 1 k+1 k + 1 next[j + 1] = next[j] + 1P 0 , P k − 1 , P k P_0,~P_{k-1},~P_k P 0 , P k − 1 , P k k' = next[k] ,找到一个字符 P k ′ P_{k'} P k ′ ′ D ′ 'D' ′ D ′ P k ′ = P j P_{k'}~=~P_j P k ′ = P j P 0 , P k ′ − 1 , P k ′ ≠ P j − k ′ , P j − 1 , P j P_0,~P_{k'-1},~P_{k'}~\not=~P_{j-k'},~P_{j-1},~P_j P 0 , P k ′ − 1 , P k ′ = P j − k ′ , P j − 1 , P j k ′ − 1 k'-1 k ′ − 1 next[j + 1] = k' + 1 = next[k'] + 1k ′ k' k ′ P k ′ = ′ D ′ P_{k'}~=~'D' P k ′ = ′ D ′ next[j + 1] = 0
# 为何递归 k = next_k 就能找到长度更短的前缀后缀 ?这归根到 n e x t next n e x t P 0 , P k − 1 , P k P_0,~P_{k-1},~P_k P 0 , P k − 1 , P k P j − k , P j − 1 , P j P_{j-k},~P_{j-1},~P_j P j − k , P j − 1 , P j P k ≠ P j P_k~ \not= P_j P k = P j p [ n e x t [ k ] ] p[next[k]] p [ n e x t [ k ] ] P j P_j P j p [ n e x t [ n e x t [ k ] ] ] p[next[next[k]]] p [ n e x t [ n e x t [ k ] ] ] P j P_j P j k = next[k] ,直到要么找到长度更短的相同前缀后缀,要么没有长度更短的相同前缀后缀。
# 代码
C++ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 #include <stdio.h> #include <string.h> void KMPSearch (char * pat, char * txt) int M = strlen (pat); int N = strlen (txt); int next[M]; computeNextArray (pat, M, next); int i = 0 ; int j = 0 ; while (i < N) { if (pat[j] == txt[i]) { i++; j++; } if (j == M) { printf ("Found pattern at index %d\n" , i - j); j = next[j - 1 ]; } else if (i < N && pat[j] != txt[i]) { if (j != 0 ) { j = next[j - 1 ]; } else { i++; } } } } void computeNextArray (char * pat, int M, int * next) int len = 0 ; next[0 ] = 0 ; int i = 1 ; while (i < M) { if (pat[i] == pat[len]) { len++; next[i] = len; i++; } else { if (len != 0 ) { len = next[len - 1 ]; } else { next[i] = 0 ; i++; } } } } int main () char txt[] = "ABABABAB" ; char pat[] = "AB" ; KMPSearch (pat, txt); return 0 ; }
C++ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 #include <stdio.h> #include <string.h> const int N = 1e6 + 10 ;char s[N], p[N];int next[N];void creatNext (char *s, int *next) next[0 ] = 0 ; int len = 0 , i = 1 ; while (i < strlen (s)) { if (s[i] == s[len]) next[i++] = ++len; else { if (len != 0 ) len = next[len - 1 ]; else next[i++] = 0 ; } } } void kmp (char *s, char *p) int i = 0 , j = 0 , n = strlen (s), m = strlen (p); while (i < n) { if (s[i] == p[j]) i++, j++; if (j == m) { printf ("%d " , i - j); j = next[j - 1 ]; } else if (i < n && s[i] != p[j]) { if (j != 0 ) j = next[j - 1 ]; else i++; } } } int main () scanf ("%s%s" , s, p); creatNext (p, next); kmp (s, p); }