首页 程序设计 杂题集

# G

# 题目大意

给定 A=(a1,...,an)A = (a_1, ..., a_n)，有 qq 个询问，每次询问给出 x,yx, y，求满足 ai=x,aj=y,x<ya_i = x, a_j = y, x < y 的 (i,j)(i, j) 对数

# 数据范围

  • 1≤n,q≤1051 \le n, q \le 10^5

# 题解

对于给定的数据，存一个 PIIPII {a[i], i} ，然后按 1. 值；2. idx sortsort 一遍
对于每次查询 (x,y)(x, y)，我们可以利用二分找到 lx,rxlx, rx 和 ly,ryly, ry
遍历其中一个，然后在另一个里去再用二分找满足 ix<iyi_x < i_y 的

以上是我赛时想出的思路，但是这有个什么问题呢，会猛猛 TLETLE
我们可以加个记忆化，存储已经查询过的 (x,y)(x,y)，然后就能 ACAC 了

C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
#include <bits/stdc++.h>
#define int long long
using namespace std;

typedef pair<int, int> PII;

int n, q, x, y;
vector<PII> a;
map<PII, int> mp;

int find_L(int x) {
    int l = 1, r = n, res = -1;

    while (l <= r) {
        int mid = l + r >> 1;

        if (a[mid].first >= x)
            res = mid, r = mid - 1;
        else
            l = mid + 1;
    }

    if (res == -1)
        return -1;

    return (a[res].first == x ? res : -1);
}

int find_R(int x) {
    int l = 1, r = n, res = -1;

    while (l <= r) {
        int mid = l + r >> 1;

        if (a[mid].first > x)
            r = mid - 1;
        else
            res = mid, l = mid + 1;
    }

    if (res == -1)
        return -1;

    return (a[res].first == x ? res : -1);
}

int find_idx(int idx, int l, int r) {
    int res = -1;
    while (l <= r) {
        int mid = l + r >> 1;

        if (a[mid].second <= idx)
            l = mid + 1;
        else
            res = mid, r = mid - 1;
    }

    return res;
}

void solve() {
    cin >> n >> q, a = vector<PII>(n + 1);
    for (int i = 1; i <= n; i++)
        cin >> a[i].first, a[i].second = i;
    
    sort(a.begin() + 1, a.end(), [](PII x, PII y) {
        return (x.first == y.first ? x.second < y.second : x.first < y.first);
    });
    
    while (q--) {
        cin >> x >> y;
        int t = mp[{x, y}];
        if (t) {
            cout << t << '\n';
            continue;
        }
        
        int lx = find_L(x), rx = find_R(x), ly = find_L(y), ry = find_R(y);
        
        if (lx == -1 || ly == -1) {
            cout << 0 << '\n';
            continue;
        }
        
        int res = 0;
        for (int i = lx; i <= rx; i++) {
            int t = find_idx(a[i].second, ly, ry);
            if (t == -1)
                break;
            res += ry - t + 1;
        }
        
        mp[{x, y}] = res;
        cout << res << '\n';
    }
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);

    int _ = 1;
    // cin >> _;

    while (_--)
        solve();

    return 0;
}

# A

# 题目大意

给定整数 n,mn, m，问你以其中 (0→n,0→m)(0 \to n, 0 \to m) 为顶点，最多能在画布中绘出几个不同的正方形

# 数据范围

  • 1≤n,m≤1051 \le n, m \le 10^5
  • 1≤n×m≤3×1051 \le n \times m \le 3 \times 10^5

# 题解

赛时是暴力枚举 + 超屎二分，赛后看了看，正解是差分

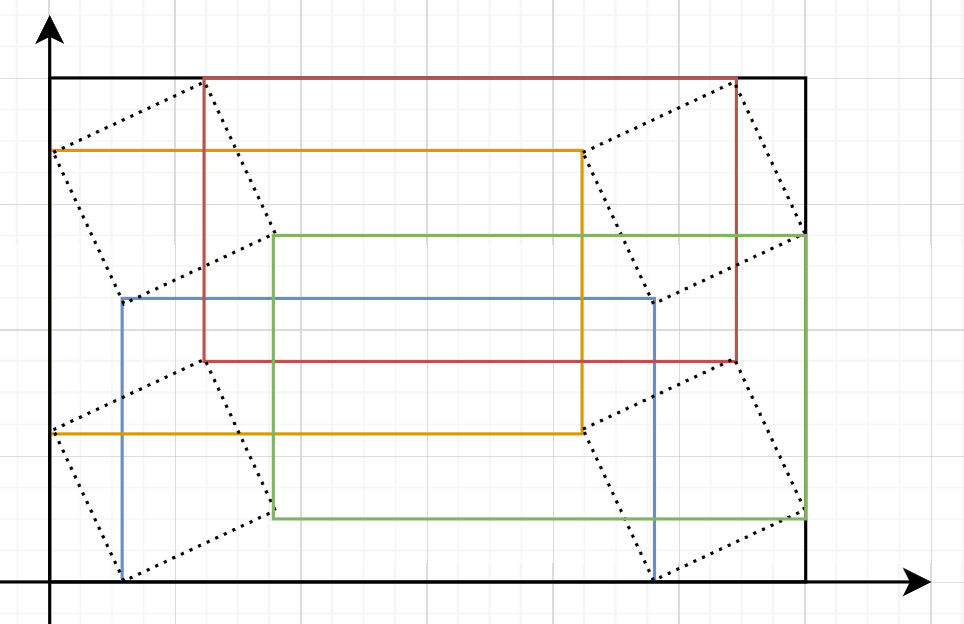
如下图所示，枚举

每种样子的正方形，会有四个贡献矩阵，对这四个贡献矩阵用差分去加一即可

C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <bits/stdc++.h>
#define int long long
using namespace std;

int n, m;
vector<vector<int>> g;

void add(int u, int l, int d, int r) {
    g[u][l]++, g[u][r]--, g[d][l]--, g[d][r]++;
}

void solve() {
    cin >> n >> m;
    n++; m++;
    g.assign(n + 1, vector<int>(m + 1, 0));

    for (int a = 0; a < min(n, m); a++) {
        for (int b = 1; a + b < min(n, m); b++) {
            auto work = [&](int l, int u) {
                int r = m - a - b + l;
                int d = n - b - a + u;
                add(u, l, d, r);
            };

            work(0, a);
            work(b, 0);
            work(a, a + b);
            work(a + b, b);
        }
    }

    for (int i = 0; i < n; i++)
        for (int j = 0; j < m; j++) {
            if (i)
                g[i][j] += g[i-1][j];
            if (j)
                g[i][j] += g[i][j-1];
            if (i && j)
                g[i][j] -= g[i-1][j-1];
        }

    for (int i = 0; i < n; i++)
        for (int j = 0; j < m; j++)
            cout << g[i][j] << (j == m-1 ? '\n' : ' ');
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    solve();
    return 0;
}