# 卷积# 一维卷积连续域函数卷积
g ( x ) = f ( x ) ∗ k ( x ) = ∫ − ∞ + ∞ f ( t ) ⋅ k ( x − t ) ⋅ d t g(x)=f(x)*k(x)=\int_{-\infty}^{+\infty}{f(t)·k(x-t)·dt} g ( x ) = f ( x ) ∗ k ( x ) = ∫ − ∞ + ∞ f ( t ) ⋅ k ( x − t ) ⋅ d t
离散函数卷积
g ( i ) = f ( i ) ∗ k ( i ) = ∑ l f ( l ) ⋅ k ( i − l ) g(i)=f(i)*k(i)=\sum\limits_{l}f(l)·k(i-l) g ( i ) = f ( i ) ∗ k ( i ) = l ∑ f ( l ) ⋅ k ( i − l )
# 二维卷积G ( x , y ) = I ( x , y ) ∗ K ( x , y ) = ∑ i = 1 H ∑ j = 1 W I ( i , j ) ⋅ K ( x − i , y − j ) G(x,y)=I(x,y)*K(x,y)=\sum\limits_{i=1}^{H}\sum\limits_{j=1}^{W}I(i,j)·K(x-i,y-j) G ( x , y ) = I ( x , y ) ∗ K ( x , y ) = i = 1 ∑ H j = 1 ∑ W I ( i , j ) ⋅ K ( x − i , y − j )
# 两种信号# 冲激信号
py 1 2 3 4 5 6 7 8 9 10 11 a = [0 , 1 , 2 , 3 , 1 , 0 ] k = [0 , 1 , 0 ] k_size = 15 k1 = np.zeros((k_size, k_size)) mid = k_size // 2 k1[mid][mid] = 1
# 方波信号
py 1 2 3 4 5 6 7 8 a = [0 , 1 , 2 , 3 , 2 , 1 , 0 ] k = [1 , 1 , 1 , 1 , 1 ] k_size = 15 k1 = 1 / k_size / k_size * np.ones((k_size, k_size))
# 图像噪声# 椒盐噪声
py 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 def add_Salt (img, percent ): noise = np.random.uniform(0 , 1 , img[:, :, 0 ].shape) salt_mask = noise < percent salt_mask = np.expand_dims(salt_mask, axis=2 ) salt_mask = np.repeat(salt_mask, 3 , axis=2 ) img = img * (1 - salt_mask) + 255 * salt_mask pepper_mask = noise > 1 - percent pepper_mask = np.expand_dims(pepper_mask, axis=2 ) pepper_mask = np.repeat(pepper_mask, 3 , axis=2 ) img = img * (1 - pepper_mask) + 0 * pepper_mask return img.astype(np.uint8)
# 高斯噪声
py 1 2 3 4 5 6 7 8 def add_Gaussian (img, sigma=20 , mean=0 ): lab = cv2.cvtColor(img, cv2.COLOR_BGR2LAB) noise = np.random.normal(mean, sigma, lab[:, :, 0 ].shape) lab = lab.astype(float ) lab[:, :, 0 ] = lab[:, :, 0 ] + noise lab[:, :, 0 ] = np.clip(lab[:, :, 0 ], 0 , 255 ) lab = lab.astype(np.uint8) return cv2.cvtColor(lab, cv2.COLOR_LAB2BGR)
# 滤波技术# 均值滤波利用方波信号作为卷积核
K = 1 k 2 [ 1 ⋯ 1 ⋮ ⋮ 1 ⋯ 1 ] k × k \boldsymbol{K}=\frac{1}{k^{2}}\left[\begin{array}{ccc} 1 &\cdots &1\\ \vdots &&\vdots\\ 1 &\cdots &1 \end{array}\right]_{k\times k} K = k 2 1 ⎣ ⎢ ⎢ ⎡ 1 ⋮ 1 ⋯ ⋯ 1 ⋮ 1 ⎦ ⎥ ⎥ ⎤ k × k
对上述添加了高斯噪声的图片进行均值滤波,得到
# 高斯滤波高斯滤波卷积核为
G ( i , j ) = 1 2 π σ 2 e − i 2 + j 2 2 σ 2 G(i,j)=\frac{1}{2\pi \sigma^2}e^{-\frac{i^2+j^2}{2\sigma^2}} G ( i , j ) = 2 π σ 2 1 e − 2 σ 2 i 2 + j 2
py 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 def gaussian_kernel (k_size, sigma ): k = np.zeros((k_size, k_size)) center = k_size // 2 s = sigma ** 2 sum_val = 0 for i in range (k_size): for j in range (k_size): x, y = i - center, j - center k[i, j] = np.exp(-(x ** 2 + y ** 2 ) / (2 * s)) / (2 * np.pi * s) sum_val += k[i, j] return k / sum_val
# 双边滤波图像 I I I I ^ \hat{I} I ^
I ^ ( i , j ) = 1 W s b ∑ m = i − k i − 1 ∑ n = j − k j − 1 I ( m , n ) ⋅ G ( i − m , j − n ) ⋅ G ( I ( m , n ) − I ( i , j ) ) \hat{I}(i,j)=\frac{1}{W_{sb}}\sum\limits_{m=i-k}^{i-1}\sum\limits_{n=j-k}^{j-1}I(m,n)·G(i-m,j-n)·G(I(m,n)-I(i,j)) I ^ ( i , j ) = W s b 1 m = i − k ∑ i − 1 n = j − k ∑ j − 1 I ( m , n ) ⋅ G ( i − m , j − n ) ⋅ G ( I ( m , n ) − I ( i , j ) )
其中
G_s(i,j)=\frac{1}{2\pi\sigma_s^2}e^{-\frac{i^2+j^2}{2\sigma^2}}$$$$G_b(d)=\frac{1}{2\pi\sigma_b^2}e^{-\frac{d^2}{2\sigma_b^2}}
W s b = ∑ m = i − k i − 1 ∑ n = j − k j − 1 G s ( i − m , j − n ) ⋅ G b ( ∣ I ( m , n ) − I ( i , j ) ∣ ) W_{sb}=\sum\limits_{m=i-k}^{i-1}\sum\limits_{n=j-k}^{j-1}G_s(i-m,j-n)·G_b(|I(m,n)-I(i,j)|) W s b = m = i − k ∑ i − 1 n = j − k ∑ j − 1 G s ( i − m , j − n ) ⋅ G b ( ∣ I ( m , n ) − I ( i , j ) ∣ )
经双边滤波后,得到图像
py 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 def bilateral_filter_custom (img, k_size=5 , sigma_s=5 , sigma_r=25 ): img = img.astype(np.float32) half = k_size // 2 h, w = img.shape img_pad = np.pad(img, ((half, half), (half, half)), mode='reflect' ) output = np.zeros_like(img, dtype=np.float32) Gs = gaussian_kernel(k_size, sigma_s) for i in range (h): for j in range (w): region = img_pad[i : i + k_size, j : j + k_size] center_val = img_pad[i + half, j + half] Gr = np.exp(-((region - center_val) ** 2 ) / (2 * sigma_r ** 2 )) Gr /= (2 * np.pi * sigma_r ** 2 ) W = Gs * Gr output[i, j] = np.sum (W * region) / (np.sum (W) + 1e-8 ) return np.clip(output, 0 , 255 ).astype(np.uint8)
# 中值滤波祛痘 是美颜时常用的操作,痘 → \to →
py 1 2 3 4 5 6 7 8 9 10 11 12 13 14 def median_filter (img, k_size ): img = img.astype(np.float32) half = k_size // 2 h, w = img.shape res = np.zeros_like(img, dtype=np.float32) img = np.pad(img, ((half, half), (half, half)), mode='reflect' ) for i in range (h): for j in range (w): region = img[i : i + k_size, j : j + k_size] res[i, j] = np.median(region) return np.clip(res, 0 , 255 ).astype(np.uint8)
# 图像锐化图像平滑是过滤掉高频信息,保留低频信息,图像锐化是反其道而行
py 1 2 3 4 5 6 7 8 9 10 11 12 13 k_size = 3 k0 = np.zeros((k_size, k_size)) center = k_size // 2 k0[center][center] = 1 kg = gaussian_kernel(k_size, 1 ) k_sharpen = 1 * (k0 - kg) img = cv2.imread('avatar_Gaussian.jpg' ) conv = conv_2d(img, k_sharpen) conv.plot_conv()
而我们不妨,在原图的基础上,加上上面的卷积核,
k_sharpen = k0 + 1 * (k0 - kg)这样我们就能使得图像锐化
由此可见,将原图减去高斯滤波后的图像,即图像的高频信息,反复叠加在原图上,可以不断增强锐化效果
# 图像匹配# 匹配步骤模板图像 T ( w × h ) T~(w\times h) T ( w × h ) I ( W × H ) I~(W \times H) I ( W × H )
让模板图像在输入图像上滑动,对于每个滑动位置,计算相似度 滑动结束后,得到相似度矩阵 R R R ( i , j ) (i,j) ( i , j ) # 相似度度量# 互相关R ( i , j ) = ∑ m = i i + 2 − 1 ∑ n = j j + h − 1 I ( m , n ) ⋅ T ( m − i , n − j ) R(i,j)=\sum\limits_{m=i}^{i+2-1}\sum\limits_{n=j}^{j+h-1}I(m,n)·T(m-i,n-j) R ( i , j ) = m = i ∑ i + 2 − 1 n = j ∑ j + h − 1 I ( m , n ) ⋅ T ( m − i , n − j )
py 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 def COR (img, tmp ): w, h = tmp.shape W, H = img.shape img = np.array(img, dtype=np.float32) tmp = np.array(tmp, dtype=np.float32) res = np.zeros((W - w + 1 , H - h + 1 ), dtype=np.float32) for i in range (W - w + 1 ): for j in range (H - h + 1 ): patch = img[i : i + w, j : j + h] res[i, j] = np.sum (tmp * patch) return res class Tmp_match (): def __init__ (self, img, tmp ): self .img = img self .tmp = tmp def match (self ): img_gray = cv2.cvtColor(self .img, cv2.COLOR_BGR2GRAY) tmp_gray = cv2.cvtColor(self .tmp, cv2.COLOR_BGR2GRAY) w, h = tmp_gray.shape res = COR(img_gray, tmp_gray) loc = np.unravel_index(np.argmax(res), res.shape) top = [int (loc[1 ]), int (loc[0 ])] bottom = [top[0 ] + h, top[1 ] + w] cv2.rectangle(self .img, tuple (top), tuple (bottom), (0 , 255 , 0 ), 2 ) plt.imshow(cv2.cvtColor(self .img, cv2.COLOR_BGR2RGB)) plt.title("Template Matching Result" ) plt.axis('off' ) plt.show() img = cv2.imread('avatar.jpg' ) tmp = cv2.imread('img.png' ) test = Tmp_match(img, tmp) test.match ()
我们发现,这个代码匹配很容易出问题,匹配到奇奇怪怪的地方
因为互相关是模板图像像素值和输入图像子图像素值直接相乘,那么模板一定的情况下,子图整体像素值越大(越亮),乘积越大,因此更容易找到亮度高的地方,而不是相似的地方
# 归一化互相关R ( i , j ) = ∑ m ∑ n I ( m , n ) ⋅ T ( m − i , n − j ) ∑ m ∑ n I 2 ( m , n ) ⋅ ∑ m ∑ n T 2 ( m − i , n − j ) R(i,j)=\frac{\sum\limits_{m}\sum\limits_{n}I(m,n)·T(m-i,n-j)}{\sqrt{\sum\limits_{m}\sum\limits_{n}I^2(m,n)}·\sqrt{\sum\limits_{m}\sum\limits_{n}T^2(m-i,n-j)}} R ( i , j ) = m ∑ n ∑ I 2 ( m , n ) ⋅ m ∑ n ∑ T 2 ( m − i , n − j ) m ∑ n ∑ I ( m , n ) ⋅ T ( m − i , n − j )
py 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 def COR (img, tmp ): w, h = tmp.shape W, H = img.shape img = np.array(img, dtype=np.float32) tmp = np.array(tmp, dtype=np.float32) res = np.zeros((W - w + 1 , H - h + 1 ), dtype=np.float32) t = np.sqrt(np.sum (tmp ** 2 )) for i in range (W - w + 1 ): for j in range (H - h + 1 ): patch = img[i : i + w, j : j + h] res[i, j] = np.sum (tmp * patch) res[i, j] = res[i, j] / t / np.sqrt(np.sum (patch ** 2 )) return res
# 多目标模板匹配
py 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 import randomimport cv2import matplotlib.pyplot as pltimport numpy as npdef findKth (s, k ): def select (arr, k ): idx = random.randint(0 , len (arr) - 1 ) pivot = arr[idx] low = [x for x in arr if x > pivot] equal = [x for x in arr if x == pivot] high = [x for x in arr if x < pivot] if k < len (low): return select(low, k) elif k < len (low) + len (equal): return pivot else : return select(high, k - len (low) - len (equal)) flat = s.flatten().tolist() if k < 1 or k > len (flat): raise ValueError("k 超出范围" ) return select(flat, k - 1 ) class MultiMatch (): def __init__ (self, img, tmp, k ): self .img = img self .tmp = tmp self .k = k def match (self ): img_gray = cv2.cvtColor(self .img, cv2.COLOR_BGR2GRAY) tmp_gray = cv2.cvtColor(self .tmp, cv2.COLOR_BGR2GRAY) h, w = tmp_gray.shape res = cv2.matchTemplate(img_gray, tmp_gray, cv2.TM_CCORR_NORMED) threshold = findKth(res, self .k) loc = np.where(res >= threshold) for pt in zip (*loc[::-1 ]): cv2.rectangle(self .img, pt, (pt[0 ] + w, pt[1 ] + h), (0 , 255 , 0 ), 2 ) plt.figure(figsize=(10 , 8 )) plt.imshow(cv2.cvtColor(self .img, cv2.COLOR_BGR2RGB)) plt.axis('off' ) plt.show() img = cv2.imread('multi_match/all_mul_match.png' ) tmp = cv2.imread('multi_match/smt.png' ) matcher = MultiMatch(img, tmp, k=3 ) matcher.match ()
# 边缘检测边缘 是图像中局部亮度、纹理或颜色发生剧烈变化的位置(边缘蕴含图像中物体的形状信息和场景的结构信息)
# 数学模型给定一幅图像 I I I ( i , j ) (i,j) ( i , j )
边缘强度 E s ( i , j ∣ I ) E_s(i,j|I) E s ( i , j ∣ I ) 边缘方向 E θ ( i , j ∣ I ) E_\theta(i,j|I) E θ ( i , j ∣ I ) 图像 I I I f ( x , y ) f(x,y) f ( x , y )
∂ f ( x , y ) ∂ x = lim x → 0 f ( x + ε , y ) − f ( x − ε , y ) 2 ε \frac{\partial f(x,y)}{\partial x}=\lim_{x \to 0} \frac{f(x+\varepsilon,y)-f(x-\varepsilon,y)}{2\varepsilon} ∂ x ∂ f ( x , y ) = x → 0 lim 2 ε f ( x + ε , y ) − f ( x − ε , y )
∂ f ( x , y ) ∂ y = lim ε → 0 f ( x , y + ε ) − f ( x , y − ε ) 2 ε \frac{\partial f(x,y)}{\partial y}=\lim_{\varepsilon \to 0} \frac{f(x,y+\varepsilon)-f(x,y-\varepsilon)}{2\varepsilon} ∂ y ∂ f ( x , y ) = ε → 0 lim 2 ε f ( x , y + ε ) − f ( x , y − ε )
由于数字图像是离散的,在数字图像中最小的位置距离单位为 1 1 1 ε = 1 \varepsilon = 1 ε = 1
I x ( i , j ) = I ( i + 1 , j ) − I ( i − 1 , j ) 2 I_x(i,j)=\frac{I(i+1,j)-I(i-1,j)}{2} I x ( i , j ) = 2 I ( i + 1 , j ) − I ( i − 1 , j )
I y ( i , j ) = I ( i , j + 1 ) − I ( i , j − 1 ) 2 I_y(i,j)=\frac{I(i,j+1)-I(i,j-1)}{2} I y ( i , j ) = 2 I ( i , j + 1 ) − I ( i , j − 1 )
其中,I x , I y I_x,I_y I x , I y ( i , j ) (i,j) ( i , j ) x , y x,y x , y ∇ I ( i , j ) = [ I x ( i , j ) , I y ( i , j ) ] \nabla I(i,j)=[I_x(i,j),I_y(i,j)] ∇ I ( i , j ) = [ I x ( i , j ) , I y ( i , j ) ]
在数字图像中,对图像的一阶微分是通过一阶差分实现的
I x ( i , j ) = 1 2 ∑ m = − 1 1 ∑ n = − 1 1 I ( i − m , j − n ) ⋅ K x ( m , n ) I_x(i,j)=\frac{1}{2}\sum\limits_{m=-1}^{1}\sum\limits_{n=-1}^{1}I(i-m,j-n)·K_x(m,n) I x ( i , j ) = 2 1 m = − 1 ∑ 1 n = − 1 ∑ 1 I ( i − m , j − n ) ⋅ K x ( m , n )
I y ( i , j ) = 1 2 ∑ m = − 1 1 ∑ n = − 1 1 I ( i − m , j − n ) ⋅ K y ( m , n ) I_y(i,j)=\frac{1}{2}\sum\limits_{m=-1}^{1}\sum\limits_{n=-1}^{1}I(i-m,j-n)·K_y(m,n) I y ( i , j ) = 2 1 m = − 1 ∑ 1 n = − 1 ∑ 1 I ( i − m , j − n ) ⋅ K y ( m , n )
其中
K x = [ 0 0 0 1 0 − 1 0 0 0 ] , K y = [ 0 1 0 0 0 0 0 − 1 0 ] K_x=\begin{bmatrix} 0 & 0 & 0 \\ 1 & 0 & -1 \\ 0 & 0 & 0 \end{bmatrix},~K_y=\begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & -1 & 0 \end{bmatrix} K x = ⎣ ⎢ ⎡ 0 1 0 0 0 0 0 − 1 0 ⎦ ⎥ ⎤ , K y = ⎣ ⎢ ⎡ 0 0 0 1 0 − 1 0 0 0 ⎦ ⎥ ⎤
边缘强度 和边缘方向 分别为
E s ( i , j ∣ I ) = I x 2 ( i , j ) + I y 2 ( i , j ) E_s(i,j|I)=\sqrt{I_x^2(i,j)+I_y^2(i,j)} E s ( i , j ∣ I ) = I x 2 ( i , j ) + I y 2 ( i , j )
E θ ( i , j ∣ I ) = tan − 1 ( I y ( i , j ) I x ( i , j ) ) + π 2 E_\theta(i,j|I)=\tan^{-1}(\frac{I_y(i,j)}{I_x(i,j)})+\frac{\pi}{2} E θ ( i , j ∣ I ) = tan − 1 ( I x ( i , j ) I y ( i , j ) ) + 2 π
# 算法边缘检测算法主要有三个步骤
图像平滑 :边缘检测算法基于图像微分 ,但是图像微分对噪声很敏感图像梯度计算 :通过差分模板对平滑处理后的图像进行卷积,得到图像梯度图像边缘定位 :根据边缘强度和边缘方向进行定位# Sobel 边缘检测算法K x = [ 1 0 − 1 2 0 − 2 1 0 − 1 ] , K y = [ 1 2 1 0 0 0 − 1 − 2 − 1 ] K_x=\begin{bmatrix} 1 & 0 & -1 \\ 2 & 0 & -2 \\ 1 & 0 & -1 \end{bmatrix},~K_y=\begin{bmatrix} 1 & 2 & 1 \\ 0 & 0 & 0 \\ -1 & -2 & -1 \end{bmatrix} K x = ⎣ ⎢ ⎡ 1 2 1 0 0 0 − 1 − 2 − 1 ⎦ ⎥ ⎤ , K y = ⎣ ⎢ ⎡ 1 0 − 1 2 0 − 2 1 0 − 1 ⎦ ⎥ ⎤
如何理解 K x K_x K x
K x = [ 1 0 − 1 2 0 − 2 1 0 − 1 ] = [ 1 2 1 ] [ 1 0 − 1 ] K_x=\begin{bmatrix} 1 & 0 & -1 \\ 2 & 0 & -2 \\ 1 & 0 & -1 \end{bmatrix}=\begin{bmatrix}1 \\ 2 \\ 1\end{bmatrix}\begin{bmatrix}1 & 0 & -1\end{bmatrix} K x = ⎣ ⎢ ⎡ 1 2 1 0 0 0 − 1 − 2 − 1 ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ 1 2 1 ⎦ ⎥ ⎤ [ 1 0 − 1 ]
[1 2 -1]^T 可以理解成一个高斯滤波, [1 0 -1] 是一个差分算子
py 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 import cv2import numpy as npimport matplotlib.pyplot as pltimg = cv2.imread('scenery.jpg' ) k_x = np.array([ [1 , 0 , -1 ], [2 , 0 , -2 ], [1 , 0 , -1 ] ]) k_y = np.array([ [1 , 2 , 1 ], [0 , 0 , 0 ], [-1 , -2 , -1 ] ]) conv_x = cv2.filter2D(img, -1 , k_x) conv_y = cv2.filter2D(img, -1 , k_y) plt.imshow(conv_x[:, :, ::-1 ]) plt.imshow(conv_y[:, :, ::-1 ]) plt.axis('off' ) plt.show()
在计算边缘强度时,通常使用不开平方的近似值
E s ( i , j ∣ I ) = ∣ ∣ I x ( i , j ) ∣ ∣ + ∣ ∣ I y ( i , j ) ∣ ∣ E_s(i,j|I)=||I_x(i,j)|| + ||I_y(i,j)|| E s ( i , j ∣ I ) = ∣ ∣ I x ( i , j ) ∣ ∣ + ∣ ∣ I y ( i , j ) ∣ ∣
py 1 2 3 4 5 6 7 8 conv_x = cv2.filter2D(img, -1 , k_x) conv_y = cv2.filter2D(img, -1 , k_y) res = abs (conv_x) + abs (conv_y) plt.imshow(res[:, :, ::-1 ]) plt.axis('off' ) plt.show()
# Canny 边缘检测算法# 图像平滑σ \sigma σ σ \sigma σ 3 3 3
py 1 2 3 4 5 6 7 8 9 10 11 12 k_size = 5 sigma = 1.5 img = cv2.imread('./edge_detect/a.jpg' ) kernel = gaussian_kernel(k_size, sigma) img = cv2.filter2D(img, -1 , kernel) plt.axis('off' ) plt.imshow(img[:, :, ::-1 ]) plt.show()
# 梯度计算使用和 S o b e l Sobel S o b e l
E s ( i , j ∣ I ) = I x 2 ( i , j ) + I y 2 ( i , j ) E_s(i,j|I)=\sqrt{I_x^2(i,j)+I_y^2(i,j)} E s ( i , j ∣ I ) = I x 2 ( i , j ) + I y 2 ( i , j )
E θ ( i , j ∣ I ) = tan − 1 ( I y ( i , j ) I x ( i , j ) ) + π 2 E_\theta(i,j|I)=\tan^{-1}(\frac{I_y(i,j)}{I_x(i,j)})+\frac{\pi}{2} E θ ( i , j ∣ I ) = tan − 1 ( I x ( i , j ) I y ( i , j ) ) + 2 π
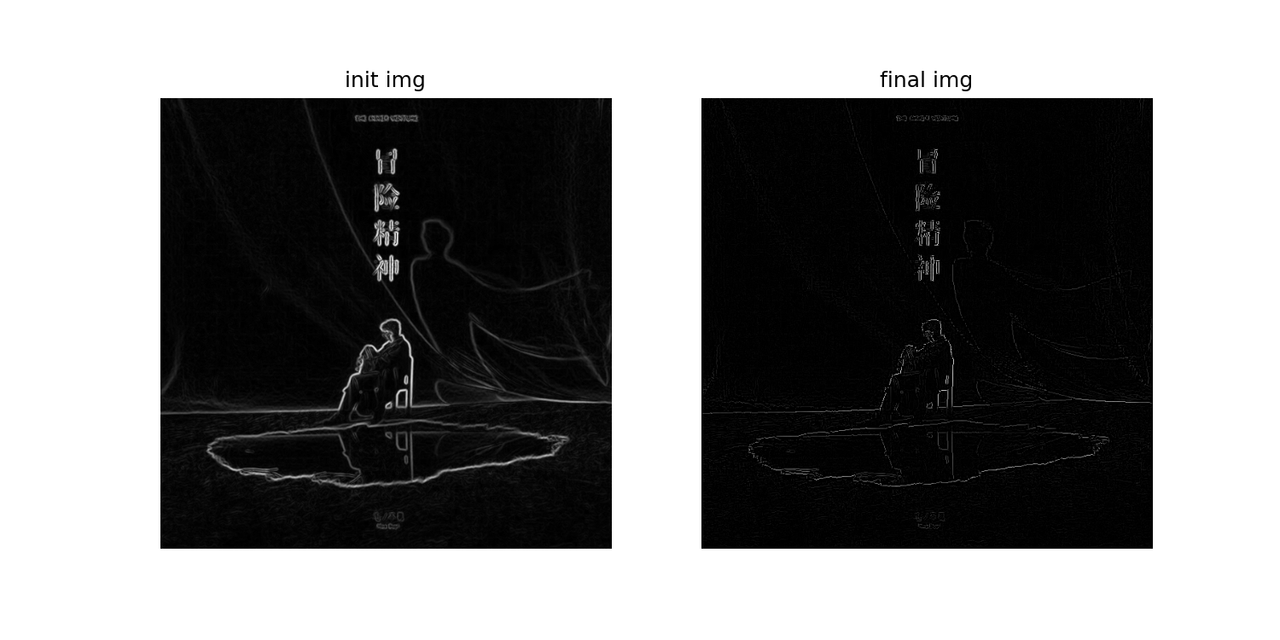
py 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 def partial_x (img ): k = np.array([ [0 , 0 , 0 ], [0.5 , 0 , -0.5 ], [0 , 0 , 0 ] ]) return cv2.filter2D(img, -1 , k) def partial_y (img ): k = np.array([ [0 , 0.5 , 0 ], [0 , 0 , 0 ], [0 , -0.5 , 0 ] ]) return cv2.filter2D(img, -1 , k) def gradient (img ): channels = [] thetas = [] for i in range (3 ): channel = img[:, :, i] dx = partial_x(channel) dy = partial_y(channel) G = np.sqrt(dx ** 2 + dy ** 2 ) theta = np.rad2deg(np.arctan2(dy, dx)) theta %= 360 channels.append(G) thetas.append(theta) G = np.maximum.reduce(channels) theta = thetas[1 ] return G, theta img = img.astype(np.float32) G, theta = gradient(img) plt.subplot(1 , 2 , 2 ) plt.axis('off' ) plt.title('final img' ) plt.imshow(G, cmap='gray' ) plt.show()
直接从梯度得到的边缘线很粗,显得很模糊,因此需要通过
非极大值抑制 将边缘细化
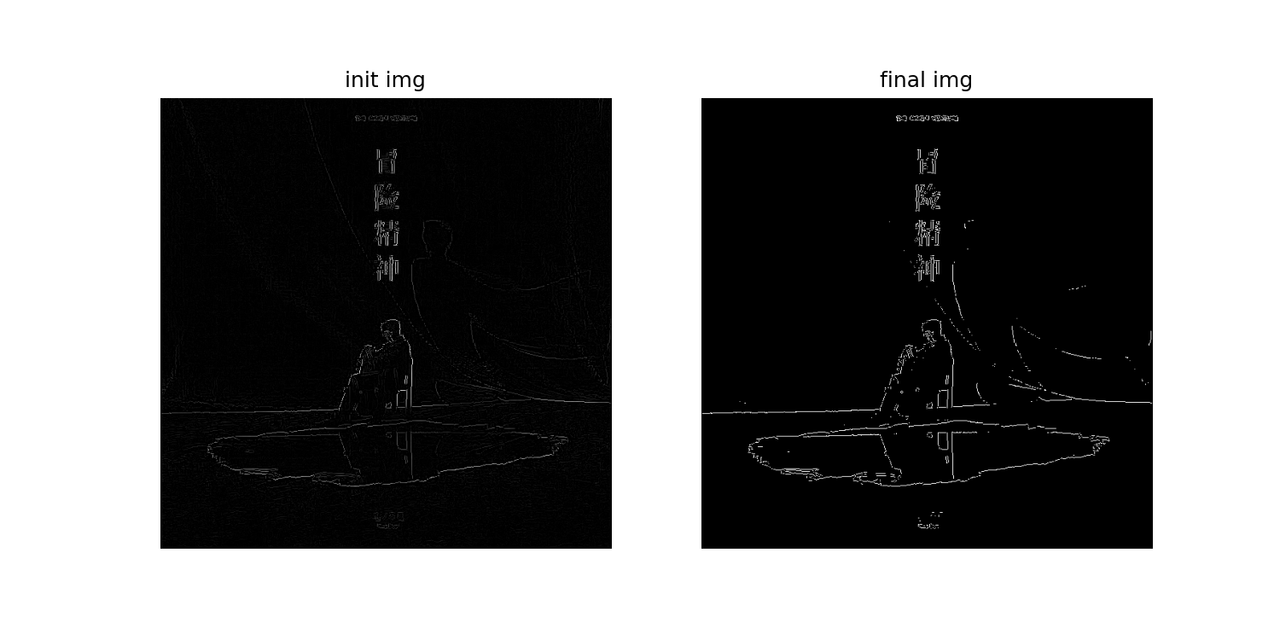
非极大值抑制 沿每个梯度方向找到边缘强度局部极大的像素予以保留,去除该方向上边缘强度非局部极大的像素
# 边缘强度非极大值抑制
py 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 def non_max_suppress (G, theta ): h, w = G.shape res = np.zeros((h, w)) theta = theta % 180 for i in range (1 , h - 1 ): for j in range (1 , w - 1 ): a = theta[i, j] now = G[i, j] if 0 <= a <= 22.5 or 157.5 <= a <= 180 : n1 = G[i, j + 1 ] n2 = G[i, j - 1 ] elif 22.5 <= a < 67.5 : n1 = G[i - 1 , j + 1 ] n2 = G[i + 1 , j - 1 ] elif 67.5 <= a < 112.5 : n1 = G[i - 1 , j] n2 = G[i + 1 , j] else : n1 = G[i - 1 , j - 1 ] n2 = G[i + 1 , j + 1 ] if now >= n1 and now >= n2: res[i, j] = now else : res[i, j] = 0 return res
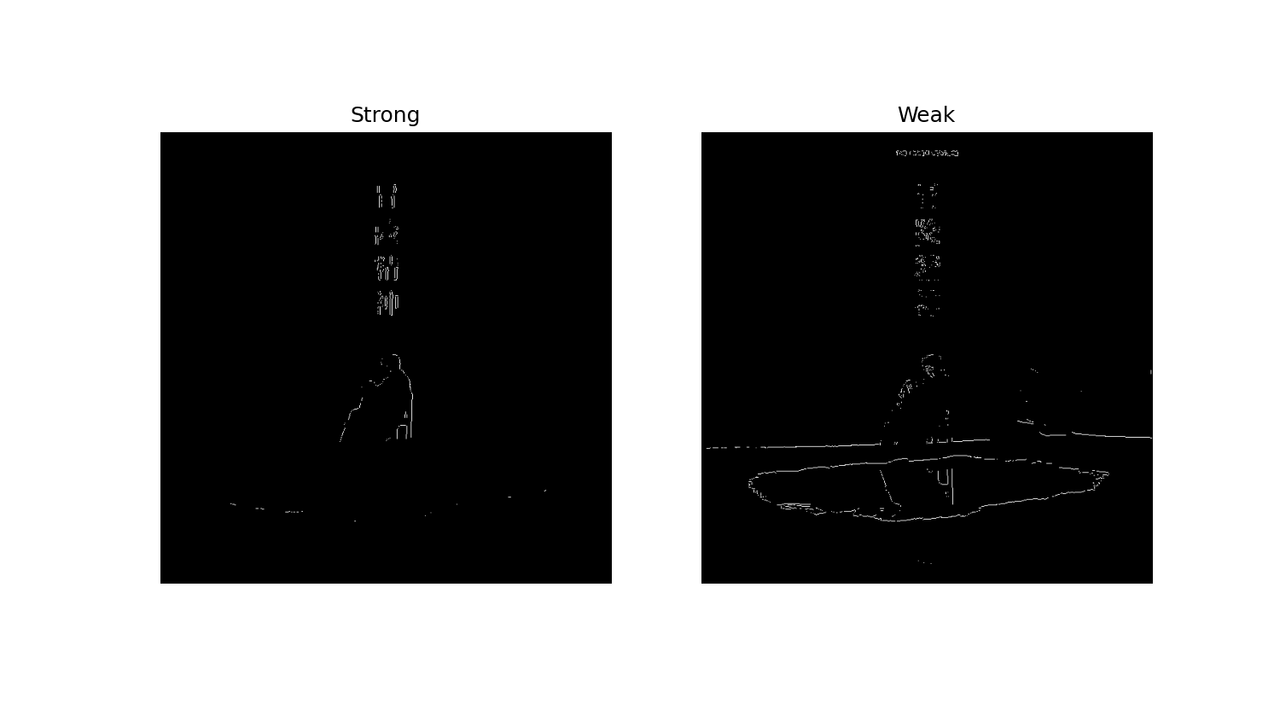
# 基于滞后的阈值化的边缘定位经过非极大值抑制后,将边缘细化成边缘线,接下来我们要确定边缘的位置E s E_s E s E b E_b E b E b ( i , j ∣ I ) = 1 E_b(i,j | I)=1 E b ( i , j ∣ I ) = 1 ( i , j ) (i,j) ( i , j )
E b ( i , j ∣ I ) = { 1 , E s ( i , j ∣ I ) ≥ T 0 , E s ( i , j ∣ I ) < T E_b(i,j|I)=\begin{cases}1, & E_s(i,j|I) \ge T \\ 0, & E_s(i,j | I) < T\end{cases} E b ( i , j ∣ I ) = { 1 , 0 , E s ( i , j ∣ I ) ≥ T E s ( i , j ∣ I ) < T
E b ( i , j ∣ I ) = { 1 , E s ( i , j ∣ I ) ≥ T h 0 , E s ( i , j ∣ I ) < T l u n k n o w , T l ≤ E s ( i , j ∣ I ) < T h E_b(i,j|I)=\begin{cases}1, & E_s(i,j | I) \ge T_h \\ 0, & E_s(i,j | I) < T_l \\ unknow,& T_l \le E_s(i,j | I) < T_h \end{cases} E b ( i , j ∣ I ) = ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ 1 , 0 , u n k n o w , E s ( i , j ∣ I ) ≥ T h E s ( i , j ∣ I ) < T l T l ≤ E s ( i , j ∣ I ) < T h
当且仅当 它们在已经确定的边缘点的领域内,才能被确定为边缘点
# 强弱边缘点的合并
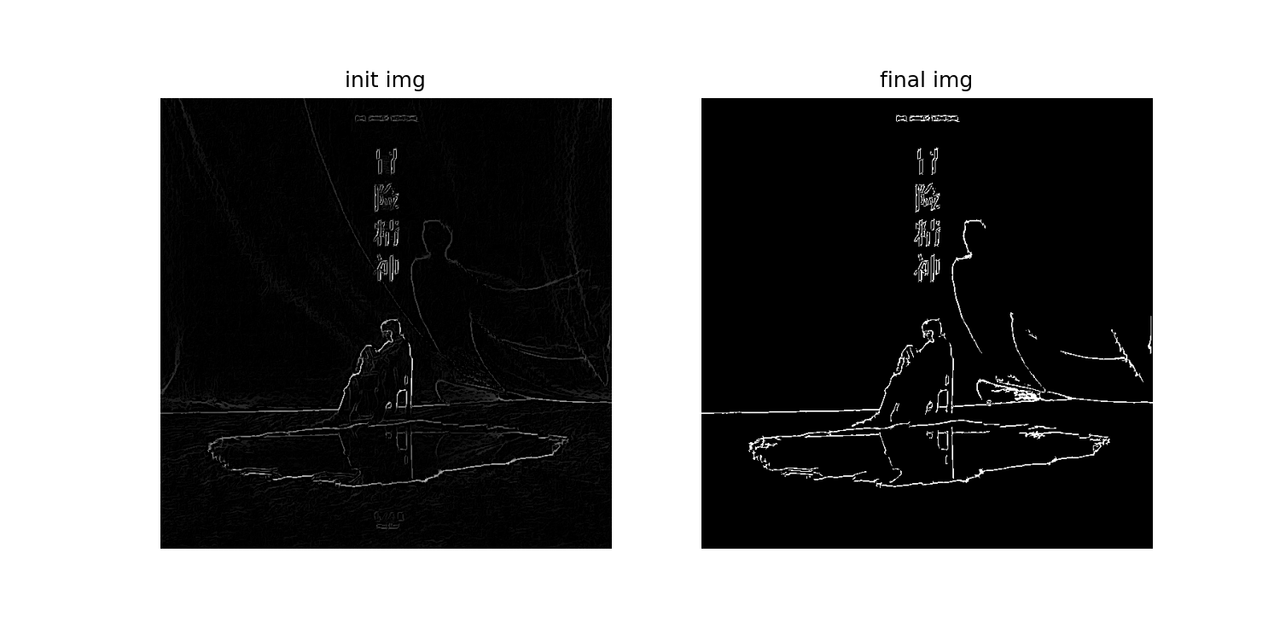
py 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 def merge_edge (strong_res, weak_res ): res = np.zeros(strong_res.shape) res[strong_res] = 255 keep = weak_res.copy() flag = True while flag: flag = False for i in range (1 , res.shape[0 ] - 1 ): for j in range (1 , res.shape[1 ] - 1 ): if keep[i, j] and not res[i, j]: if np.any (res[i - 1 : i + 2 , j - 1 : j + 2 ] == 255 ): res[i, j] = 255 flag = True return res
可能效果还不如
S o b e l Sobel S o b e l ,但是边缘(明显的边缘)更精准
# 角点检测前面提到,模板匹配是最基础、最简单的图像匹配(模板和待匹配子图必须有极高相似度)。那么一般情况下的图像匹配如何实现呢?这需要检测图像中的特征进行匹配,局部特征通常被称为关键点特征 或者兴趣点特征 ,他们有以下四个性质
# Harris 角点检测算法对于图像每个 位置,计算窗口移动前后其内部的像素值变化量 计算像素值变化量对应的角点响应函数,并对该函数进行阈值处理,提取角点 # 计算像素值变化量在图像 I I I W W W ( u , v ) (u,v) ( u , v ) E ( u , v ) E(u,v) E ( u , v )
E ( u , v ) = ∑ ( i , j ) ∈ W ( I ( i + u , j + v ) − I ( i , j ) ) 2 E(u,v)=\sum\limits_{(i,j) \in W}(I(i+u, j+v)-I(i,j))^2 E ( u , v ) = ( i , j ) ∈ W ∑ ( I ( i + u , j + v ) − I ( i , j ) ) 2
如果窗口位于平坦区域,无论位置 ( u , v ) (u,v) ( u , v ) E ( u , v ) E(u,v) E ( u , v ) 位于边缘时,沿着边缘移动,E ( u , v ) E(u,v) E ( u , v ) 当位于角点的时候,无论往哪移动,E ( u , v ) E(u,v) E ( u , v ) 利用泰勒展开获取近似形式 I ( i + u , j + v ) ≈ I ( i , j ) + u I x + v I y I(i+u,j+v) \approx I(i,j)+uI_x+vI_y I ( i + u , j + v ) ≈ I ( i , j ) + u I x + v I y I x , y I_{x,y} I x , y x , y x,y x , y
E ( u , v ) = ∑ ( i , j ) ∈ w ( u 2 I x 2 + v 2 I y 2 + 2 u v I x I y ) E(u,v)=\sum\limits_{(i,j) \in w}(u^2I_x^2+v^2I_y^2+2uvI_xI_y) E ( u , v ) = ( i , j ) ∈ w ∑ ( u 2 I x 2 + v 2 I y 2 + 2 u v I x I y )
提出 ( u , v ) (u,v) ( u , v )
E ( u , v ) = [ u v ] M [ u v ] E(u,v) = \begin{bmatrix}u & v\end{bmatrix} M \begin{bmatrix}u \\ v\end{bmatrix} E ( u , v ) = [ u v ] M [ u v ]
矩阵 M M M
M = ∑ ( i , j ) ∈ W [ I x 2 I x I y I x I y I y 2 ] \boldsymbol{M} = \sum_{(i,j) \in \boldsymbol{W}} \begin{bmatrix} I_{x}^{2} & I_{x}I_{y} \\ I_{x}I_{y} & I_{y}^{2} \end{bmatrix} M = ( i , j ) ∈ W ∑ [ I x 2 I x I y I x I y I y 2 ]
M = ∑ ( i , j ) ∈ w H M=\sum\limits_{(i,j) \in w}H M = ( i , j ) ∈ w ∑ H H H H I I I 黑塞矩阵
M = R [ λ 1 0 0 λ 2 ] R T M=R\begin{bmatrix} \lambda_1 & 0 \\ 0 & \lambda_2 \end{bmatrix}R^{T} M = R [ λ 1 0 0 λ 2 ] R T
其中,λ 1 , λ 2 \lambda_1,\lambda_2 λ 1 , λ 2 M M M R R R E ( u , v ) E(u,v) E ( u , v )
E ( u , v ) = [ u v ] R [ λ 1 0 0 λ 2 ] R ⊤ [ u v ] E(u,v) = \begin{bmatrix} u & v \end{bmatrix}\boldsymbol{R}\begin{bmatrix} \lambda_1 & 0 \\ 0 & \lambda_2 \end{bmatrix}\boldsymbol{R}^\top\begin{bmatrix} u \\ v \end{bmatrix} E ( u , v ) = [ u v ] R [ λ 1 0 0 λ 2 ] R ⊤ [ u v ]
令 [ m n ] = [ u v ] R [m~n]=[u~v]R [ m n ] = [ u v ] R
E ( u , v ) = [ m n ] [ λ 1 0 0 λ 2 ] [ m n ] ⊤ = m 2 λ 1 + n 2 λ 2 E(u,v) = \left[\begin{array}{ll} m & n \end{array}\right] \left[\begin{array}{cc} \lambda_{1} & 0 \\ 0 & \lambda_{2} \end{array}\right] \left[\begin{array}{ll} m & n \end{array}\right]^{\top} = m^{2}\lambda_{1} + n^{2}\lambda_{2} E ( u , v ) = [ m n ] [ λ 1 0 0 λ 2 ] [ m n ] ⊤ = m 2 λ 1 + n 2 λ 2
由此,像素值变化量 E ( u , v ) E(u,v) E ( u , v ) M M M
# 计算角点响应函数角点附近的 E ( u , v ) E(u,v) E ( u , v ) ( u , v ) (u,v) ( u , v ) [ m n ] = [ u v ] R [m~n]=[u~v]R [ m n ] = [ u v ] R
m 2 + n 2 = [ m n ] [ m n ] = [ u v ] R R ⊤ [ u v ] = u 2 + v 2 m^{2}+n^{2}= \left[\begin{array}{ll} m & n \end{array}\right] \left[\begin{array}{l} m \\ n \end{array}\right]= \left[\begin{array}{ll} u & v \end{array}\right] \boldsymbol{R}\boldsymbol{R}^{\top} \left[\begin{array}{l} u \\ v \end{array}\right]= u^{2}+v^{2} m 2 + n 2 = [ m n ] [ m n ] = [ u v ] R R ⊤ [ u v ] = u 2 + v 2
假设微小位移 ( u , v ) (u,v) ( u , v ) u 2 + v 2 ≈ 1 → u 2 + v 2 ≈ 1 u^2+v^2 \approx 1 \to u^2 + v^2 \approx 1 u 2 + v 2 ≈ 1 → u 2 + v 2 ≈ 1
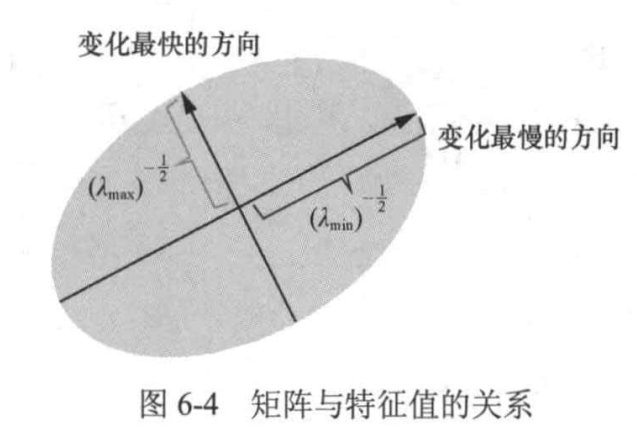
max u , v E ( u , v ) = m a x ( λ 1 , λ 2 ) \max_{u,v}E(u,v)=max(\lambda_1,\lambda_2) u , v max E ( u , v ) = m a x ( λ 1 , λ 2 )
min u , v E ( u , v ) = m i n ( λ 1 , λ 2 ) \min_{u,v}E(u,v)=min(\lambda_1,\lambda_2) u , v min E ( u , v ) = m i n ( λ 1 , λ 2 )
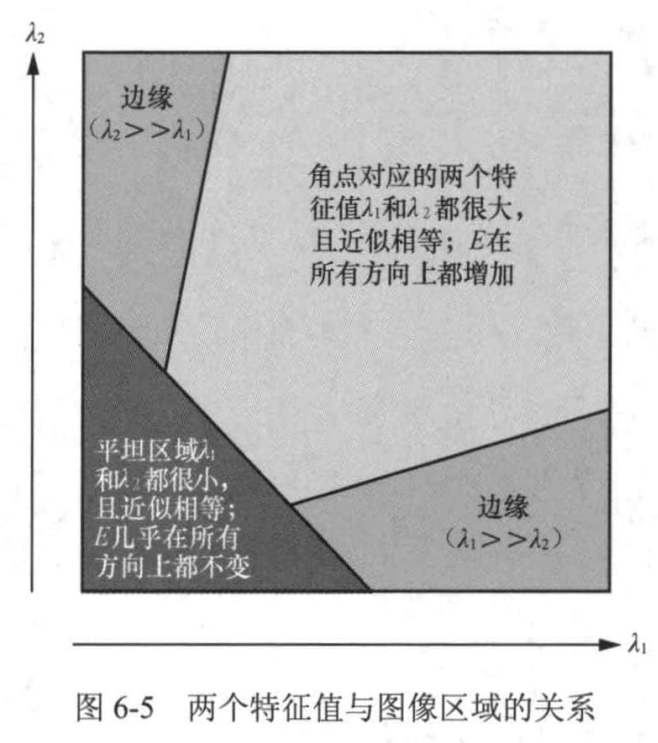
两个特征值都小,且近似相等 :对应图像平坦区域一个大、一个小,且相差较大 :对应图像边缘区域两个都大,且近似相等 :对应图像角点虽然可以根据大小关系判断角点,但是我们还是希望通过一个单一的度量指标,根据经验,提出下方角点响应函数
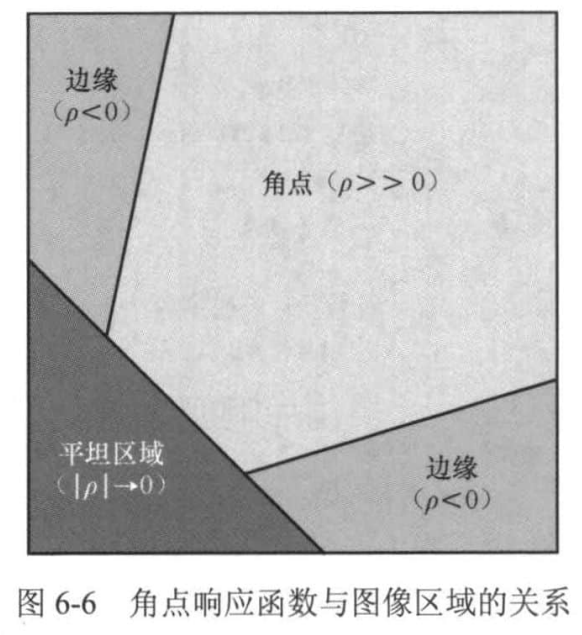
ρ = λ 1 λ 2 − α ( λ 1 + λ 2 ) 2 \rho = \lambda_1 \lambda_2 - \alpha (\lambda_1 + \lambda_2)^2 ρ = λ 1 λ 2 − α ( λ 1 + λ 2 ) 2
其中,α \alpha α 0.04 → 0.06 0.04 \to 0.06 0 . 0 4 → 0 . 0 6
ρ = λ 1 λ 2 − α ( λ 1 + λ 2 ) 2 = det ( M ) − α trace ( M ) 2 \rho = \lambda_{1}\lambda_{2} - \alpha(\lambda_{1}+\lambda_{2})^{2} = \det(\boldsymbol{M}) - \alpha \operatorname{trace}(\boldsymbol{M})^{2} ρ = λ 1 λ 2 − α ( λ 1 + λ 2 ) 2 = det ( M ) − α t r a c e ( M ) 2
计算出 ρ \rho ρ γ \gamma γ ρ > γ \rho > \gamma ρ > γ
# 代码实现
C++ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 import cv2import matplotlib.pyplot as pltimport numpy as npfrom tools import * # 角点响应函数 def response (M) : # 超参数 k = 0.04 det = np.linalg.det (M) trace = np.trace (M) # 角点响应函数 R = det - k * trace ** 2 return R # Harris 角点检测算法 def harris (img, NMS=True): h, w = img.shape[:2 ] img = cv2. cvtColor (img, cv2. COLOR_BGR2GRAY) point = np.zeros ((h, w)) grad = np.zeros ((h, w, 2 ), dtype=np.float32) grad[:, :, 0 ] = cv2. Sobel (img, cv2. CV_16S, 1 , 0 ) grad[:, :, 1 ] = cv2. Sobel (img, cv2. CV_16S, 0 , 1 ) Ix = grad[:, :, 0 ] ** 2 Iy = grad[:, :, 1 ] ** 2 Ixy = grad[:, :, 0 ] * grad[:, :, 1 ] Ix = cv2. GaussianBlur (Ix, (3 , 3 ), sigmaX=2 ) Iy = cv2. GaussianBlur (Iy, (3 , 3 ), sigmaX=2 ) Ixy = cv2. GaussianBlur (Ixy, (3 , 3 ), sigmaX=2 ) for i in range (img.shape[0 ]): for j in range (img.shape[1 ]): # 构建 M 矩阵 sm = [[Ix[i, j], Ixy[i, j]], [Ixy[i, j], Iy[i, j]]] # 计算角点响应函数 R = response (sm) point[i, j] = R # 非极大值抑制 corner = np.zeros_like (img, dtype=np.float32) threshold = 0.01 maxVal = np.max (point) for i in range (point.shape[0 ]): for j in range (point.shape[1 ]): if NMS: if point[i][j] > threshold * maxVal \ and point[i][j] == np.max (point[max (0 , i - 1 ) : min (i + 1 , h - 1 ), max (0 , j - 1 ) : min (j + 1 , w - 1 )]): corner[i, j] = 255 else : if point[i][j] > threshold * maxVal: corner[i, j] = 255 return corner if __name__ == "__main__" : img = cv2. imread ("./img/qp.png" ) # 可以先进行锐化(锐化可以提高角点检测的效果) k_size = 3 k0 = np.zeros ((k_size, k_size)) center = k_size k0[center][center] = 1 kg = gaussian_kernel (k_size, 1 ) k_sharpen = k0 + 1 * (k0 - kg) conv = conv_2d (img, k_sharpen) for i in range (2 ): img = conv.conv (img, k_sharpen) conv = conv_2d (img, k_sharpen) plt.imshow (img[:, :, ::-1 ]) plt.axis ('off' ) plt.title ("Original Image" ) response = harris (img) img[response == 255 ] = [0 , 0 , 255 ] plt.imshow (img[:, :, ::-1 ]) plt.axis ('off' ) plt.title ("Harris Corner" ) plt.show ()
# 基于尺度空间的块状区域检测的基本原理由上一小章可以知道,角点对于尺度是不变的
随着高斯拉普拉斯算子标准差增大,当高斯拉普拉斯算子 的标准差大小和块状区域 大小相同时,他们的卷积结果会出现唯一极值点,此时记为 σ ∗ \sigma^{*} σ ∗ σ \sigma σ x x x ( x , σ ) (x, \sigma) ( x , σ )
出现这种现象,是因为高斯拉普拉斯算子的响应会随着标准差的变大而衰减,因此需要对响应做归一化,即对其乘以 σ 2 \sigma^2 σ 2
在归一化后,此时特征尺度下的极值点是整个 ( x , σ ) (x,\sigma) ( x , σ ) ( x , σ ) (x,\sigma) ( x , σ )
# 迁移到图像中图像的尺度空间 L ( x , y , σ ) L(x,y,\sigma) L ( x , y , σ ) G ( x , y , σ ) G(x,y,\sigma) G ( x , y , σ ) I ( x , y ) I(x,y) I ( x , y ) ( x , y , σ ) (x,y,\sigma) ( x , y , σ ) L ( x , y , σ ) L(x,y,\sigma) L ( x , y , σ )
L ( x , y , σ ) = G ( x , y , σ ) ∗ I ( x , y ) L(x,y,\sigma)=G(x,y,\sigma) * I(x,y) L ( x , y , σ ) = G ( x , y , σ ) ∗ I ( x , y )
由滤波的知识可知
σ \sigma σ σ \sigma σ 如果找到了两幅图像中对应的特征点,对特征点对应的特征尺度求比值,就可以得到两幅图像尺度缩放的比例
# SIFT 算法![]()
![]()
![]()
![]()
![]()
![]()