写在前面
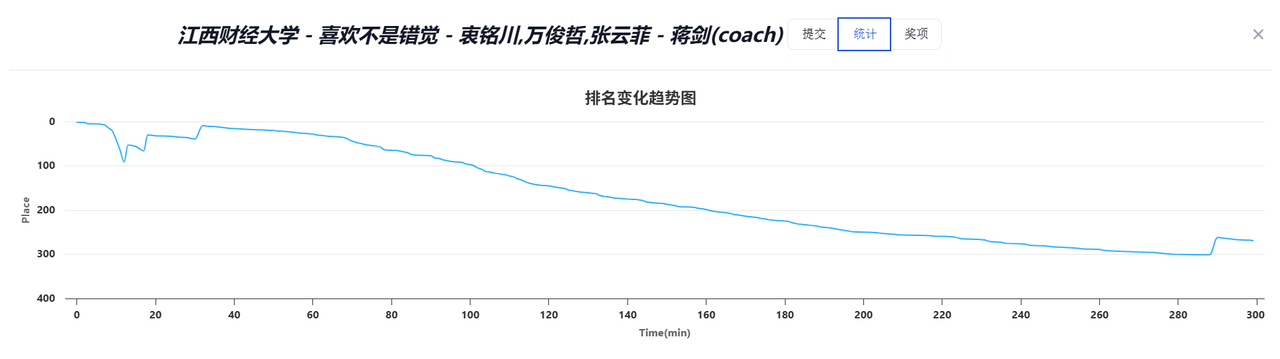
第一次打铁的一集，离铜就差一点点（少几发罚时，或者多开一题其实就过了，全员战犯的一集，看漏题目，~~我是 memset 战犯~~）

这个时候离铜尾已经很近了，一直在想着说能不能在最后拿块铜，结果还是罚时太长，可能有一部分决策问题吧，~~喜欢不是错觉不是本人~~，只能遗憾下机
热身赛成分复杂，第一次在体育馆里比赛，场馆很气派，不羡鸳鸯不羡仙，只羡 AC 弹指间
前 $30mins$ 开题其实挺快的，~~还以为能突破拿银了~~
[补题链接][https://codeforces.com/gym/105941]

# D

# 题目大意

判断一个数

本身是不是完全平方数
各位数字之和是不是完全平方数

# 数据范围

$1 \le y \le 999999$

# 题解

手速题

C++

bool check(int n) {
    int t = sqrt(n);
    return t * t == n;
}

void solve () {
    string s;
    cin >> s;
    int n = 0, nn = 0;
    for (auto c : s)
        n += (c - '0'), nn = nn * 10 + (c - '0');

    cout << (check(n) && check(nn) ? "Yes" : "No") << '\n';
}

# M

# 题目大意

现在给你 $n$ 个点 $m$ 条边，你可以选择创建或销毁一条通路，请问，最少需要经过多少次操作后，图可以变成一个无向树

# 数据范围

$1 \le n \le 10^6$
$0 \le m \le 10^6$

# 题解

这题还挺容易漏考虑情况的，首先，很容易想到的情况是

重遍
自环

这可以很容易用并查集解决，只要新来的边的两个点，祖宗节点相同，则不允连边

那么还有以下两种情况

孤立点
多个孤立集合

为什么是两种呢，因为孤立点也可以看作一个孤立集合，显然，在多个孤立集合（每个集合都是一个无向树）之间，要使得整个图变成一个无向树，只需要再多连 孤立集合个数 - 1 条边即可，赛时一把过，赛后 $WA$ 三发

C++

int n, m, cnt;
vector<int> f(N);
vector<bool> flag(N);

int find(int u) {
    return (u == f[u] ? f[u] : f[u] = find(f[u]));
}

void solve () {
    cin >> n >> m, cnt = 0;

    for (int i = 1; i <= n; i++)
        f[i] = i;
    
    for (int i = 1, u, v; i <= m; i++) {
        cin >> u >> v;

        int fu = find(u), fv = find(v);

        if (fu == fv) {
            cnt++;
            continue;
        }

        f[fu] = fv, flag[u] = flag[v] = 1;
    }

    int t = 0;

    set<int> father;
    for (int i = 1; i <= n; i++)
        father.insert(find(i));

    cout << cnt + father.size() - 1 << '\n';
}

# J

# 题目大意

给你一个由大写字母构成的字符串 $S$ ，你可以任意进行凯撒移位（具体地说，选择任意一个非负数 $k$ ，然后对于 $S$ 中的每个字母加上 $k$ 然后取模 $26$ ，得到新字母），给定一个 洞 的概念（我也不知道是什么），反正就有个对应关系
int holes[26] = {1, 2, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0};
请你计算，最多可以得到多少 洞

# 数据范围

$1 \le |S| \le 10^6$

# 题解

暴力枚举 $k$

C++

void solve () {
    cin >> s;
    int maxx = 0;

    for (int k = 0; k < 26; k++) {
        int res = 0;
        for (int i = 0; i < s.size(); i++)
            res += holes[(s[i] - 'A' + k) % 26];

        maxx = max(maxx, res);
    }

    cout << maxx << '\n';
}

# H

# 题目大意

初始时，有无穷个孤立的结点，第 $i$ 个结点的编号为 $i$
树论函数的定义为： $f(n)=n \times (n+1)$ ，若存在 $f(n)=f(a) \times f(b)$ ，则由结点 $n$ 出发，分别向 $a,b$ 建立一条无向边

现在，若从结点 $s$ 出发，则 $[l, r]$ 中，有多少个点是 $s$ 可达的？

# 数据范围

$1 \le T \le 10^5$
$1 \le s \le 10^9$
$1 \le l \le r \le 10^9$

# 题解

赛时其实是打表找规律写出来的，通过打表可以发现，对于 $f(i) \times f(i+1)$ ，我总是能在后面找到一个 $f(n) = f(i) \times f(i + 1)$ ，由此猜测，所有点都是连起来的，答案就是 r - l + 1 ，严谨的数学证明如下
$f(x) \times f(x+1)=x(x+1)(x+1)(x+2)$
又有 $x(x+2) = x^2+2x = (x+1)^2 - 1$
所以， $f(x) \times f(x+1) = [x(x+2)] \times [x(x+2)+1] = f[x(x+2)]$ ，得证

C++

void solve () {
    int a, b, c;
    cin >> a >> b >> c;
    cout << (c - b + 1) << '\n';
}

# G

# 题目大意

你现在需要构造一个 $n$ 个点的树，使得其最大独立集大小等于直径长度

最大独立集：在树中最多能选出的，两两不相邻的点数
直径长度：两个点之间最长的简单路径包含的边数

# 数据范围

$1 \le T \le 5 \times 10^4$
$2 \le n \le 10^5$

# 题解

赛后补题的时候，又犯了和赛时一样的错误，当 $n=2$ 时，是可以构造出树来的
构造如下

SHOW

// n = 2
1 - 2

// n = 3
1 - 2 - 3

// n = 4
非法

// n = 5
1 - 2 - 3 - 4
	    |
	    5

// n = 7
1 - 2 - 3 - 4 - 5
        |   |
        6   7

由此便可继续推导了，当 n 是奇数时，先构造出
..... - x - x
        |
        x

那么当 n += 2 时候，往最右边的下方和右边分别接一个
..... - x - x - k
        |   |
        x   k

显然可以知道，此时直径是增加了 1 的
而点数由于本身最右边的 x 是点，又接了两个 k 后，显然让两个 k 变成点，x 抛弃，也就是说增加了 2 - 1 = 1 个点，
增加的直径 = 增加的点数，故符合题意，可以构造

而针对偶数，我们只需要构造好其 -1 的奇数，然后把 n 接在最左端即可
如 n = 6，先行构造 n = 5
1 - 2 - 3 - 4
        |
        5

接上 6

6 - 1 - 2 - 3 - 4
			|
			5

在奇数图左边接上一个点，直径显然 +1
而先行构造好的奇数图而言，最左端的 1 是不作为点而存在的，接上 n 后，点数也显然 +1
增加的直径 = 增加的点数，故符合题意，可以构造

代码如下所示

C++

void solve () {
    cin >> n;

    if (n == 4) {
        cout << -1 << '\n';
        return;
    }

    if (n == 2) {
        cout << "1 2\n";
        return;
    }

    int flag = (n & 1 ? 0 : n);

    // 确保 
    if (!(n & 1))
        n--;

    int t = (n - 1) / 2 + 2;

    for (int i = 2; i <= t; i++)
        cout << i - 1 << ' ' << i << '\n';

    for (int i = t + 1, k = 3; i <= n; i++, k++)
        cout << i << ' ' << k << '\n';
    
    if (flag)
        cout << "1 " << flag << '\n';
}

以后写这种构造题一定要注意， $n$ 为 $1 \to 3$ 的时候，也就是最小的那几个样例，一定不能想当然地认为它 true 或 false ，一定要自己构造出来，万般确定之后，再去考虑后面的情况，不然就算后面的构造对了，也是 $WA$ ，而且前面错了较难发现，像这题，在赛时就一直没考虑 $2$ ，一直以为是自己构造错了，从而一直修改后面， $WA$ 了几发，要是和前面一样一发 $A$ 就铜了

以上五题是赛时开的题目，有点手速题的感觉，下面是赛后补的题

# F

# 题目大意

给定 $n \times m$ 的迷宫，每个格子为 .（空地） 或 #（障碍） ，你从 $(1, 1)$ 出发，目标是到达右下角 $(n,m)$ ，每次可以上、下、左、右移动一格，你可以至多服用一次药剂，在服用后的连续 $k$ 步中，你可以把障碍物视为空地
请你计算，从起点移动到终点， $k$ 的最小值是多少

# 数据范围

$1 \le T \le 2.5 \times 10^5$
$2 \le n,m \le 1000$
保证 $\sum{(nm)} \le 10^6$

# 题解

题目要求，服用药剂后，是连续 $k$ 步，所以我们最优的走法，肯定是走到左上角 . 的边缘，然后经过若干个 . / # ，到达右下角 . 的边缘，所以我们可以先做两遍 $BFS$ ，把左下角和右下角连续的 . 保留为 . ，其他都视为 #
然后从 $(1, 1)$ 点开始做 $0-1BFS$

遇到 . $push\_front$ ，需要的 $k$ 为上一步的 $k$
遇到 # $push\_back$ ，需要的 $k$ 为上一步的 $k + 1$

这题就是我战犯的题目， memset 真的太慢了，从现在开始，只要有频繁 memset 的都换成重新 $vector$ 开，这里对了就铜牌了

C++

typedef pair<int, int> PII;
const int N = 1e3 + 10;

int dx[] = {0, 1, -1, 0, 0};
int dy[] = {0, 0, 0, 1, -1};

int n, m;


bool check(int x, int y) {
    return (x >= 1 && x <= n && y >= 1 && y <= m && !st[x][y]);
}

void bfs(int x, int y) {
    queue<PII> q;
    q.push({x, y}), st[x][y] = 1;

    while (q.size()) {
        auto [x, y] = q.front();
        q.pop();

        fg[x][y] = '.';

        for (int i = 1; i <= 4; i++) {
            int xx = x + dx[i], yy = y + dy[i];

            if (check(xx, yy)) {
                if (g[xx][yy] == '.')
                    q.push({xx, yy}), st[xx][yy] = 1;
            }
        }
    }
}

vector<vector<char>> g, fg;
vector<vector<bool>> st;

void solve() {
    cin >> n >> m;
    g = vector<vector<char>>(n + 1, vector<char>(m + 1));
    fg = vector<vector<char>>(n + 1, vector<char>(m + 1, '#'));
    st = vector<vector<bool>>(n + 1, vector<bool>(m + 1, 0));

    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            cin >> g[i][j];

    bfs(1, 1), bfs(n, m);

    deque<PII> dq;
    st = vector<vector<bool>>(n + 1, vector<bool>(m + 1, 0));
    vector<vector<int>> k(n + 1, vector<int>(m + 1, 0));

    dq.push_back({1, 1}), st[1][1] = 1;

    while (dq.size()) {
        auto [x, y] = dq.front();
        dq.pop_front();

        for (int i = 1; i <= 4; i++) {
            int xx = x + dx[i], yy = y + dy[i];

            if (check(xx, yy)) {
                if (fg[xx][yy] == '.')
                    dq.push_front({xx, yy}), k[xx][yy] = k[x][y];
                else
                    dq.push_back({xx, yy}), k[xx][yy] = k[x][y] + 1;
                st[xx][yy] = 1;
            }
        }
    }

    cout << k[n][m] << '\n';
}

# E

# 题目大意

现在一共有 $2n$ 个字符串，请你把它任意地均分为两组， $A=(a_1, ..., a_n), B(b_1, ..., b_n)$

用 $pre(s_1, s_2)$ 代表两个字符串的公共前置长度

现在请你计算， $\min \sum\limits_{i=1}^{n}$

# 数据范围

$1 \le n \le 10^5$
$1 \le |s| \le 10^5$
$\sum |s| \le 2 \times 10^5$

# 题解

其实题目很容易，赛时不会求这样的前缀， $trie$ 字典树，~~我们是文盲~~，把字符串数组 $sort$ 一遍，奇偶排就行
把奇数组字符串放进 $trie$ 树里，然后遍历偶数组字符串，对于每一个字符串，在已经构造好的 $trie$ 树里能很轻松的计算出它对于奇数组的所有字符串的和

C++

int n, idx = 0;

int trie[N][26], cnt[N * 26];

void insert(string& s) {
    int root = 0;

    for (int i = 0; i < s.size(); i++) {
        int t = s[i] - 'a';

        if (trie[root][t] == 0)
            trie[root][t] = ++idx;

        root = trie[root][t];
        cnt[root]++;
    }
}

int find(string &s) {
    int root = 0, res = 0;
    for (int i = 0; i < s.size(); i++) {
        int t = s[i] - 'a';

        if (trie[root][t] == 0)
            return res;

        root = trie[root][t], res += cnt[root];
    }

    return res;
}

void solve () {
    cin >> n;
    vector<string> s(2 * n + 1);
    for (int i = 1; i <= 2 * n; i++)
        cin >> s[i];
    
    sort(s.begin() + 1, s.end());

    int res = 0;
    for (int i = 1; i <= 2 * n; i += 2)
        insert(s[i]);
    for (int i = 2; i <= 2 * n; i += 2)
        res += find(s[i]);

    cout << res << '\n';
}

图论 BFS 构造并查集树 Tire树

# D

# 题目大意

# 数据范围

# 题解

# M

# 题目大意

# 数据范围

# 题解

# J

# 题目大意

# 数据范围

# 题解

# H

# 题目大意

# 数据范围

# 题解

# G

# 题目大意

# 数据范围

# 题解

# F

# 题目大意

# 数据范围

# 题解

# E

# 题目大意

# 数据范围

# 题解

2025CCPC长春邀请赛

2025ICPC武汉邀请赛