首页 学习学习我爱学习 运筹学

# 单向选择题

  1. 运输问题是一种特殊的线性规划问题，因而求解结果为以下
    A. 可能出现唯一最优解或无穷多最优解✅
    B. 只可能出现唯一最优解
    C. 可能出现唯一最优解 无穷多最优解 无可行解 无界解之一
    D. 除无可行解外，其他三个均可能出现
  2. 产销平衡运输问题，数学模型系数矩阵 Pi,jP_{i,j} 只有两个元素取值为一，其余为 00，那么这两个取一的元素位于
    A. 第 m+im+i 行和第 jj 行
    B. 第 ii 行和第 m+jm+j 行✅
    C. 第 jj 行和第 n+in+i 行
    D. 第 ii 行和第 jj 行
  3. 含有 n×mn \times m 个变量，n+mn+m 个约束条件的产销平衡问题的数学模型中，基变量的个数
    A. n×mn \times m 个
    B. 恰好为 n+m−1n+m-1 个✅
    C. ≤n+m−1\le n+m-1 个
    D. n+mn+m 个
  4. 灵敏度分析的时候，当线性规划最优解中某个基变量的系数 ai,ja_{i,j} 发生变化的时候，将其反应到最终单纯形表中可能出现的情况有
    A. 两者均为可行解 / 非可行解
    B. 原问题为非可行解，对偶问题为可行解
    C. 原问题为可行解，对偶问题为非可行解
    D. 前三个选项均有可能出现✅
  5. 灵敏度分析的时候，当线性规划目标函数的系数 cjc_j 发生变化时，将其反应到最终单纯性表中可能出现
    A. 两者均为非可行解
    B. 原问题为非可行解，对偶问题为可行解
    C. 原问题为可行解，对偶问题为非可行解✅
    D. 前三个选项均有可能出现
  6. 用单纯形法求解线性规划问题时，通常总是选取最大的正检验数对应的变量作为换入基的变量，理由是什么
    A. 可以减少迭代次数
    B. 避免出现退化
    C. 使迭代后目标函数增加值最大✅
    D. 前三个选项均不正确
  7. 线性规划可行域的顶点对应的解为
    A. 最优解
    B. 基可行解✅
    C. 可行解
    D. 基解
  8. 线性规划问题存在可行域的时候，正确的是
    A. 可能无可行解
    B. 可能出现无界解✅
    C. 存在最优解，不一定唯一
    D. 存在唯一最优解
  9. 一个求目标函数极小化的线性规划问题，如果增加一个新的约束条件，那么其目标函数的最优值将
    A. 不变
    B. 可能减小
    C. 可能增大✅
    D. 前三种均可能
  10. 图解法求解线性规划问题时，以下选项正确的是
    A. 如果存在最优解，最优解一定是可行域的某个顶点
    B. 如果存在可行域，原点一定包含在可行域内
    C. 用于表示两个变量坐标轴的单位长度必须一致
    D. 以上均不正确✅

# 判断题

  1. 线性规划问题的可行域如为最优解，则该可行解一定是基可行解（❌）
  2. 对偶问题的对偶问题一定是原问题（✅）
  3. 单纯形法的迭代过程是从一个可行解转换到目标函数值更大的另一个可行解（❌）
  4. 线性规划问题的每一个基解对应可行域的一个顶点（❌）
  5. 图解法和单纯形法虽然求解形式不同，但从几何上理解，两者一致（✅）
  6. 按最小元素法给出的初始基可行解，从每一个空格出发，可以找到而且仅能找出唯一的回路（❌）
  7. 表上作业法实际上就是求解运输问题的单纯形法（✅）
  8. 根据对偶问题的性质，当原问题为无界解的时候，其对偶问题无可行解，反之当对偶问题无可行解的时，其对偶问题具有无界解（❌）
  9. 任何线性规划问题存在，并具有唯一的对偶问题（✅）
  10. 单纯形法计算中，选取最大的正检验数对应的变量作为换入变量，将目标函数的值得到最快增长（❌）

# 简答题

  1. 关于运筹学，前英国协会会长 xxx 托木林森，提出哪六条原则（书上引言）
    1. 合伙原则：是指运筹学工作者要和各方面人，尤其是同实际部门工作者合作。
    2. 催化原则：在多学科共同解决某问题时，要引导人们改变一些常规的看法
    3. 互相渗透原则：要求多部门彼此渗透地考虑问题，而不是只局限于本部门
    4. 独立原则：在研究问题时，不应受某人或某部门的特殊政策所左右，应独立从事工作
    5. 宽容原则：解决问题的思路要宽，方法要多，而不是局限于某种特定的方法
    6. 平衡原则：要考虑各种矛盾的平衡，关系方面的平衡
  2. 求解运筹问题的工作步骤
    1. 提出和形成问题。即要弄清问题的目标，可能的约束，问题的可控变量以及有关参数，搜集有关资料
    2. 建立模型。即把问题中可控变量、参数和目标与约束之间的关系用一定的模型表示出来；
    3. 求解。用各种手段（主要是数学方法，也可用其他方法）将模型求解。解可以是最优解、次优解、满意解。复杂模型的求解需用计算机，解的精度要求可由决策者提出；
    4. 解的检验。首先检查求解步骤和程序有无错误，然后检查解是否反映现实问题；
    5. 解的控制。通过控制解的变化过程决定对解是否要作一定的改变；
    6. 解的实施。是指将解用到实际中必须考虑到实施的问题，如向实际部门讲清解的用法，在实施中可能产生的问题和修改。
  3. 运筹学的性质有哪些
    1. 运筹学的性质和特点。莫斯（P.M.Morse）和金博尔（G.E.Kimball) 曾对运筹学下的定义是：“为决策机构在对其控制下业务活动进行决策时，提供以数量化为基础的科学方法。” 它首先强调的是科学方法，这含义不单是某种研究方法的分散和偶然的应用，而是可用于整个一类问题上，并能传授和有组织的活动。它强调以量化为基础，必然要用数学。但任何决策都包含定量和定性两方面，而定性方面又不能简单地用数学表示，如政治、社会等因素，只有综合多种因素的决策才是全面的。
    2. 运筹学工作者的职责是为决策者提供可以量化方面的分析，指出那些定性因素的力度。另一定义是：“运筹学是一门应用科学，它广泛应用现有的科学技术知识和数学方法，解决实际中提出的专门问题，为决策者选择最优决策提供定量依据。” 这定义表明运筹学具有多学科交叉的特点，如综合运用经济学、心理学、物理学、化学中的一些方法。运筹学是强调最优决策，“最” 是过分理想了，在实际生活中往往用次优、满意等概念代替最优。因此，运筹学的又一定义是：“运筹学是一种给出问题坏的答案的艺术，否则的话问题的结果会更坏。”
  4. 求解运输问题时，表上作业法的具体步骤是什么
    1. 找出初始基可行解。即在有 m×nm\times n 格的产销平衡表上按一定的规则，给出 m+n−1m+n-1 个数字，称为数字格。它们就是初始基变量的取值。
    2. 求各非基变量的检验数，即在表上计算空格的检验数，判别是否达到最优解。如已是最优解，则停止计算，否则转到下一步。
    3. 确定换人变量和换出变量，找出新的基可行解。在表上用闭回路法调整。
    4. 重复 2. 3. 直到得到最优解为止。

# 计算题

# 第一题

# 题面

用单纯形法求解下面的 LPLP 问题

minZ=−3x1−4x2minZ = -3x_1-4x_2

s.t.{2x1+x2+x3=40x1+3x2+x4=30x1,x2,x3,x4≥0s.t.\begin{cases} 2x_1+x_2+x_3=40\\ x_1+3x_2+x_4=30\\ x_1,x_2,x_3,x_4 \ge 0 \end{cases}

# 题解

# 第二题

# 题面

用大 MM 法求解下面的 LPLP 问题

maxZ=2x1+3x2−5x3maxZ=2x_1+3x_2-5x_3

s.t.{x1+x2+x3=72x1−5x2+x3≥10x1,x2,x3≥0s.t.\begin{cases} x_1+x_2+x_3=7\\ 2x_1-5x_2+x_3 \ge 10 \\ x_1,x_2,x_3 \ge 0 \end{cases}

# 题解

# 第三题

# 题面

用大 MM 法求解下面的 LPLP 问题

maxZ=2x1+3x2−5x3maxZ=2x_1+3x_2-5x_3

s.t.{x1+x2+x3=72x1−5x2+x3≥10x1,x2,x3≥0s.t.\begin{cases} x_1+x_2+x_3=7\\ 2x_1-5x_2+x_3 \ge 10 \\ x_1,x_2,x_3 \ge 0 \end{cases}

# 题解

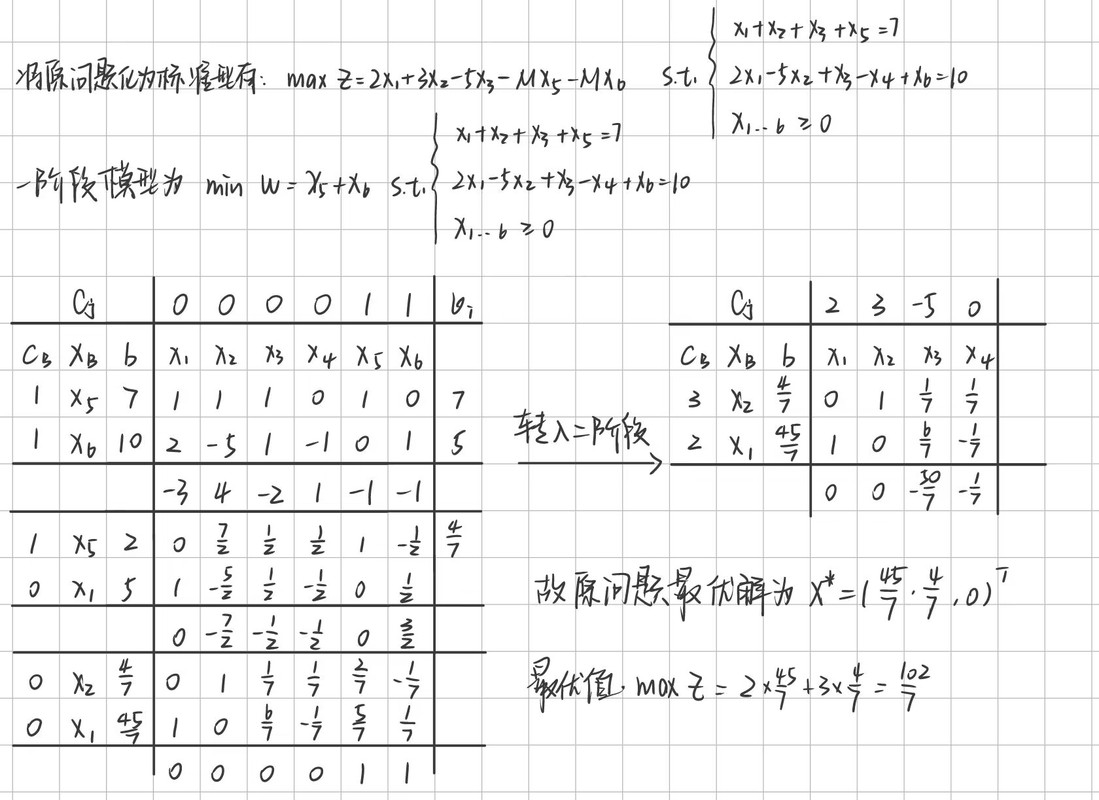
# 第四题

# 题面

已知线性规划问题

maxZ=2x1+x2+5x3+6x4maxZ=2x_1+x_2+5x_3+6x_4

s.t.{2x1+x3+x4≤82x1+2x2+x3+2x4≤12xj≥0,j=1,2,3,4s.t.\begin{cases} 2x_1+x_3+x_4\le8\\ 2x_1+2x_2+x_3+2x_4\le12\\ x_j \ge 0, j = 1, 2,3,4 \end{cases}

其对偶问题的最优解魏 y1∗=4,y2∗=1y_1^*=4, y_2^*=1，试用对偶理论求解原问题的最优解

# 题解