# 哈夫曼树的基本概念

哈夫曼树（ $Huffman$ ）树又称最优树，是一类带权路径长度最短的树

路径：从树中一个结点到另一个结点之间的分支构成这两个结点之间的路径
路径长度：路径上的分支数目称作路径长度
树的路径长度：从树根到每一结点的路径长度之和。
权：赋予某个实体的一个量，是对实体的某个或某些属性的数值化描述。在数据结构中，实体有结点（元素）和边（关系）两大类，所以对应有结点权和边权。结点权或边权具体代表什么意义，由具体情况决定。如果在一棵树中的结点上带有权值，则对应的就有带权树等概念
结点的带权路径程度：从该结点到树根之间的路径长度与结点上权的乘积
树的带权路径长度：树中所有叶子结点的带权路径长度之和，通常记作 $WPL~=~\sum_{k=1}^n w_kl_k$
哈夫曼树：假设有 $m$ 个权值 $\lbrace w_1,~w_2,~...,~w_m\rbrace$ ，可以构造一棵含 $n$ 个叶子结点的二叉树，每个叶子结点的权为 $w_i$ ，则其中带权路径长度 $WPL$ 的最小二叉树称作最优二叉树或霍夫曼树

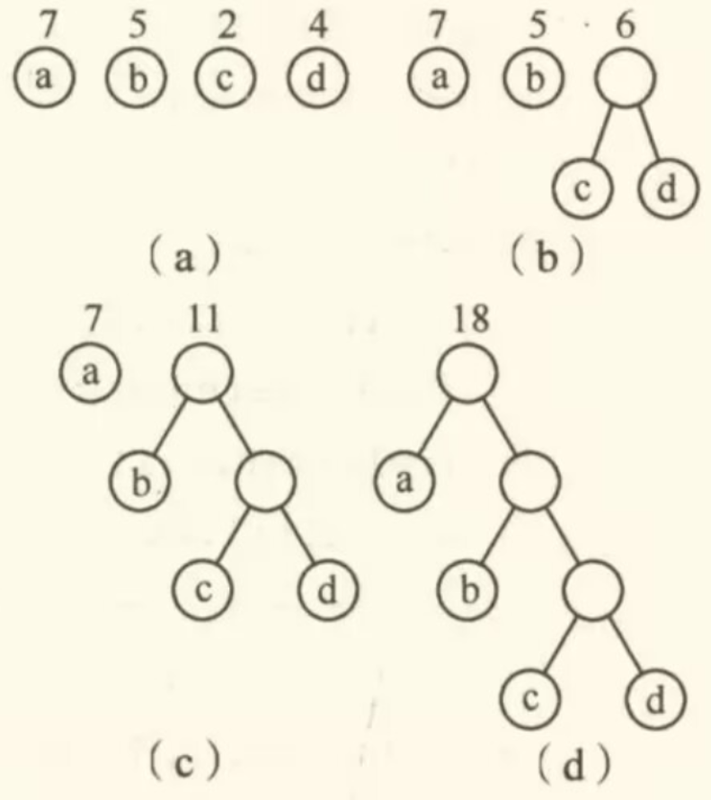
下图中， $(c)$ 树的 $WPL$ 最小，可以验证，它恰为哈夫曼树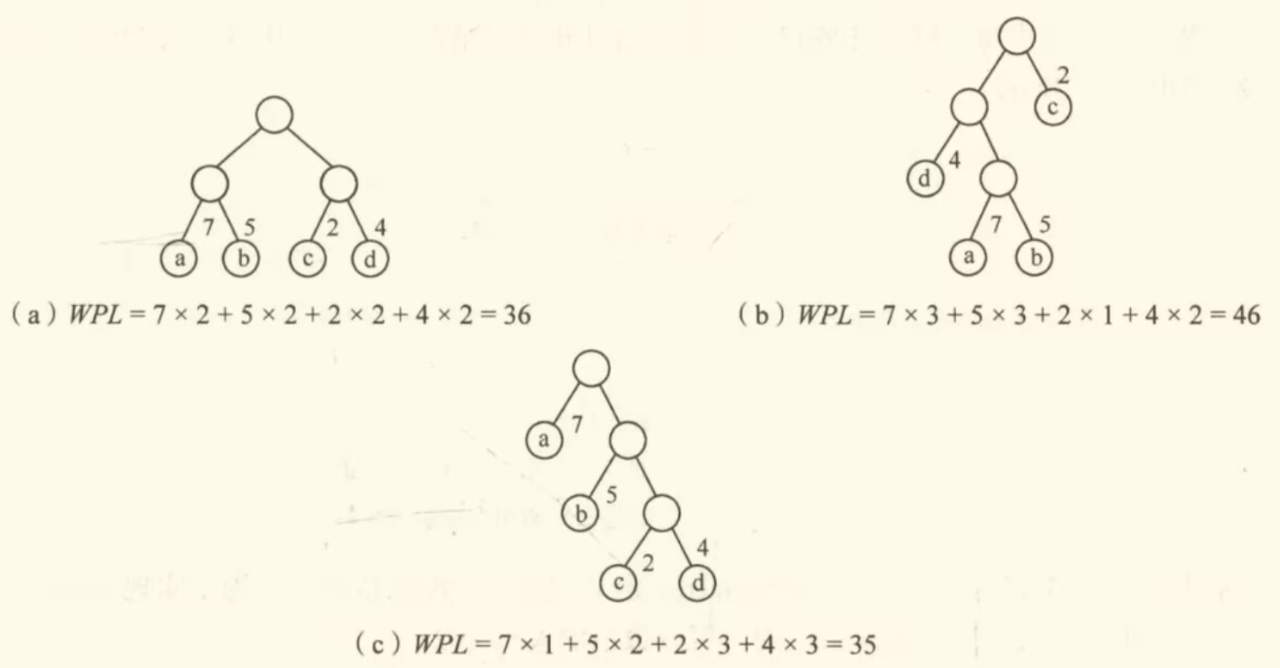

哈夫曼树中具有不同权值的叶子结点的分布有什么特点呢？从上面的例子中，可以直观地发现，在哈夫曼树中，权值越大的结点离根节点越近。根据这个特点，可以提出哈夫曼算法

# 哈夫曼树的构造算法

# 哈夫曼树的构造过程

根据给定的 $n$ 个权值 $\lbrace w_1,~...,~w_n \rbrace$ ，构造 $n$ 棵只有根节点的二叉树，这 $n$ 棵二叉树构成一个森林 $F$
在森林 $F$ 中选取两棵根节点的权值最小的树作为左右子树构造一棵新的二叉树，且置新的二叉树的根节点的权值为其左、右子树上根结点的权值之和
在森林 $F$ 中删除这两棵树，同时将新得到的二叉树加入 $F$ 中
重复上两个步骤，直到 $F$ 只含一棵树为止，这棵树便是哈夫曼树

在构造哈夫曼树时，首先选择权值小的，这样保证权值大的离根较近，这样一来，在计算树的带权路径长度时，自然会得到最小带权路径长度（贪心）

# 哈夫曼编码

在考试中，赵明诚现在要给 $zmc$ 传答案，选项一共有 $ABCD$ 四个选项，并且出现次数各不相同，则我们可以把出现次数当作叶子结点的点权，然后构造哈夫曼树，即可得出编码

数据结构哈夫曼树