指导老师：毛明松
编撰：衷铭川（大数据 231 班，程设协会负责人）、杨镇宁（大数据 241 班）
友链：其实连按部就班也比想象中难
江西财经大学信息管理与数学学院、计算机与人工智能学院程序设计竞赛协会

# 图？树？

图和树的内容，往小了说很多，往大了说就更多了。本篇文章只给出了部分基础算法，供读者参考。

# 题目

题目集链接：https://vjudge.net/contest/706652
题目集密码： $duoxichangan$
$VJ$ 比较抽象，可能需要～～魔法～～科学上网
排行榜链接：https://vjudge.net/contest/706652#rank

题目	知识点
$Make~it~Simple$	重边、自环的概念
查找文献	图的存储和遍历
【模板】拓扑排序 / 家谱树	拓扑排序
【模板】单源最短路径（标准版）	单源最短路（ $Dijkstra$ ）
【模板】Floyd	$Floyd$ 算法
【模板】最小生成树	$Prim$ 算法

# Make it Simple

# 题目大意

给你一个无向图，图中有 $N$ 个顶点和 $M$ 条边，顶点的编号为 $1$ 到 $N$ ，边的编号为 $1$ 到 $M$ 。边 $i$ 连接顶点 $u_i$ 和 $v_i$ .
要通过删除边使图形变成简单图，问必须删除的边的最少数目是多少？
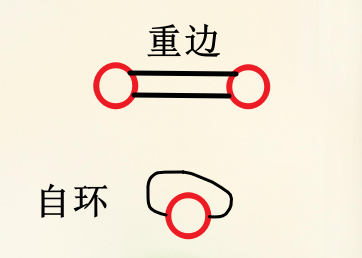
这里，当且仅当一个图不包含重边或自环时，它才被称为简单图。

# 题解

写这题，首先你需要知道重边和自环是什么东西，下面给出图例。

那这题瞬间就变得很容易了，我们只需要开一个 map<PII, bool> mp 用作标记就行，示例代码如下：

C++

void solve () {
    cin >> n >> m;
    int t = 0;
    map<PII, bool> mp;

    for (int i = 1, a, b; i <= m; i++) {
        cin >> a >> b;

        if (a == b)
            t++;
        else if (mp[{min(a, b), max(a, b)}])
            t++;
        
        mp[{min(a, b), max(a, b)}] = true;
    }

    cout << t << endl;
}

# 查找文献

# 题目大意

假设洛谷博客里面一共有 $n(n\le10^5)$ 篇文章（编号为 $1$ 到 $n$ ）以及 $m(m\le10^6)$ 条参考文献引用关系。目前小 $K$ 已经打开了编号为 $1$ 的一篇文章，请帮助小 $K$ 设计一种方法，使小 $K$ 可以不重复、不遗漏的看完所有他能看到的文章。
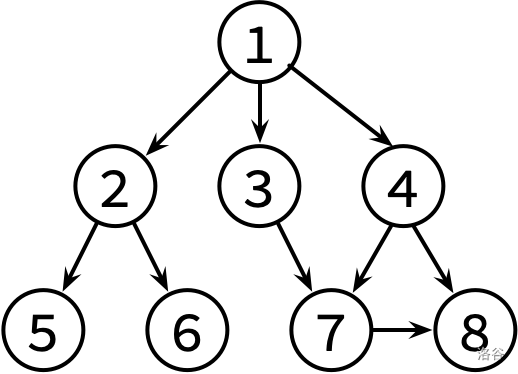
这边是已经整理好的参考文献关系图，其中，文献 $X \to Y$ 表示文章 $X$ 有参考文献 $Y$ 。不保证编号为 $1$ 的文章没有被其他文章引用。

请对这个图分别进行 $DFS$ 和 $BFS$ ，并输出遍历结果。如果有很多篇文章可以参阅，请先看编号较小的那篇（因此你可能需要先排序）。

# 题解

这题的重点是学会如何存图和遍历图，可以参考如下代码

C++

struct edge{       //存边结构体
    int u,v;
}; 
vector <int> e[100001];  
vector <edge> s;
bool vis1[100001]={0},vis2[100001]={0}; //标记数组
void dfs(int x){  //深度优先遍历
    vis1[x]=1;
    cout<<x<<" ";
    for(int i=0;i<e[x].size();i++){
        int point=s[e[x][i]].v;
        if(!vis1[point]){
            dfs(point);
        }
    }
}

void bfs(int x){  //广度优先遍历
    queue <int> q;
    q.push(x);
    cout<<x<<" ";
    vis2[x]=1;
    while(!q.empty()){
        int fro=q.front();
        for(int i=0;i<e[fro].size();i++){
            int point=s[e[fro][i]].v;
            if(!vis2[point]){
                q.push(point); 
                cout<<point<<" ";
                vis2[point]=1;
            }
        }
        q.pop();
    }
}

# 【模板】拓扑排序 / 家谱树

# 题目大意

有个人的家族很大，辈分关系很混乱，请你帮整理一下这种关系。给出每个人的后代的信息。输出一个序列，使得每个人的后辈都比那个人后列出。

# 题解

我们在小学的时候就学过事件安排的智慧，泡面前要先烧开水，烧开水前要先接水。再比如学校排课时，某些课程需要先修基础课，教务处会根据这些课程的逻辑先后关系来制定课表，这实际上就是拓扑排序的典型应用。
拓扑排序传送门.
而本题就是一个典型的拓扑排序问题，计算拓扑排序的步骤如下：

计算每个点的入度
入度为 $0$ 就加入队列

当队列不为空则循环：

取出队首元素并输出
遍历队首元素的连边，对应节点的入度 $-1$ .

当对应的节点入度为

0

就加入队列

C++

int n, a;
int rd[N];
vector<int> g[110];

void solve () {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        while (cin >> a && a != 0) {
            // i -> a
            g[i].push_back(a);
            rd[a]++;
        }
    }

    queue<int> q;
    for (int i = 1; i <= n; i++)
        if (rd[i] == 0)
            q.push(i);
    
    while (q.size()) {
        int f = q.front();
        q.pop();
        
        cout << f << " ";

        for (auto t : g[f]) {
            rd[t]--;
            if (rd[t] == 0)
                q.push(t);
        }
    }
}

# 【模板】单源最短路径（标准版）

# 题目大意

给定一个 $n$ 个点， $m$ 条有向边的带非负权图，请你计算从 $s$ 出发，到每个点的距离。
数据保证你能从 $s$ 出发到任意点。

# 数据范围

$1 \leq n \leq 10^5$
$1 \leq m \leq 2\times 10^5$
$s = 1$
$1 \leq u_i, v_i\leq n$
$0 \leq w_i \leq 10 ^ 9$
$0 \leq \sum w_i \leq 10 ^ 9$

# 题解

C++

void add(int a, int b, int c) {
	e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(0);	cout.tie(0);

	memset(h, -1, sizeof(h));
	cin >> n >> m >> s;

	for (int i = 1; i <= n; i++)	d[i] = 2147483647;

	for (int i = 1; i <= m; i++) {
		cin >> a >> b >> c;
		add(a, b, c);
	}

	d[s] = 0;

	priority_queue<PII, vector<PII>, greater<PII>> heap;
	heap.push({ 0, s });

	while (heap.size()) {
		auto t = heap.top();	heap.pop();

		int ver = t.second, dis = t.first;
		
		if (st[ver]) continue;

		st[ver] = true;

		for (int i = h[ver]; i != -1; i = ne[i]) {
			int j = e[i];
			if (d[j] > d[ver] + w[i]) {
				d[j] = d[ver] + w[i];
				heap.push({ d[j], j });
			}
		}
	}

	for (int i = 1; i <= n; i++)
		cout << d[i] << " ";
	return 0;
}

# 【模板】Floyd

# 题目大意

给 $n$ 个点和 $m$ 条边组成的无向图，求所有 $(i,j)$ 的最短路径。

# 数据范围

$n \le 100$ ， $m \le 4500$ ，任意一条边的权值 $w$ 是正整数且 $1 \le w \le 1000$ .

# 题解

Floyd 算法传送门
考察 $Floyd$ 算法的板子题 ~~（本质上是动态规划）~~ 。
f[i][j] 为从 $i$ 到 $j$ 的最短路径。
本质上是一个三维状态数组， f[i][j][k] 为从 $i$ 到 $j$ 期间经过了 $1$ 到 $k$ 这些点。

C++

void solve () {
    cin>>n>>m;
    for(int i=1;i<=n;++i)for(int j=1;j<=n;++j){
        if(i==j)dis[i][j]=0;
        else dis[i][j]=INF;
    }
    int v1,v2;ll w;
    for(int i=0;i<m;++i){
        cin>>v1>>v2>>w;
//        dis[v1][v2]=dis[v2][v1]=w;
        //取重边时较小的边 
        dis[v2][v1]=dis[v1][v2]=min(dis[v1][v2],w);
//        dis[v2][v1]=min(dis[v2][v1],w);
    }
    for(int k=1;k<=n;++k){
        for(int i=1;i<=n;++i){
            for(int j=1;j<=n;++j){
                if((i!=j)&&(i!=k)&&(j!=k))
                dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
            }
        }
    }
    for(int i=1;i<=n;++i){
        for(int j=1;j<=n;++j){
            if(j>1)cout<<" ";
            cout<<dis[i][j];
        }
        cout<<endl; 
    }

# 【模板】最小生成树

# 题目大意

给出一个无向图，求最小生成树，若图不连通，则输出 orz .

# 数据范围

$1 \le N \le 5000$ ， $1 \le M \le 2 \times 10^5$ ， $1 \le Z_i \le 10^4$ .

# 题解

观察此题数据范围，应该用 $Prim$ 算法，因数据结构课上已经讲过 $Prim$ 算法，故此处不再过多赘述。
Prim 算法参考传送门

int g[N][N], d[N], n, m;
bool st[N];

int prim() {
	int res = 0;

	for (int i = 1; i <= n; i++) {
		int t = -1;

		for (int j = 1; j <= n; j++)
			if (!st[j] && (t == -1 || d[t] > d[j]))
				t = j;

		if (t != 1 && d[t] == 0x3f3f3f3f)
			return 0x3f3f3f3f;
		
		if (t != 1)
			res += d[t];

		st[t] = true;

		for (int j = 1; j <= n; j++)
			d[j] = min(d[j], g[t][j]);
	}
	return res;
}

图论二分图 Dijkstra 最短路优先队列

# 图？树？

# 题目

# Make it Simple

# 题目大意

# 题解

# 查找文献

# 题目大意

# 题解

# 【模板】拓扑排序 / 家谱树

# 题目大意

# 题解

# 【模板】单源最短路径（标准版）

# 题目大意

# 数据范围

# 题解

# 【模板】Floyd

# 题目大意

# 数据范围

# 题解

# 【模板】最小生成树

# 题目大意

# 数据范围

# 题解

知识点复习

唯一分解定理