# 最大公约数（GCD）

# 最小公倍数（LCM）

# 图形化分析

对于复杂的、$GCD$、$LCM$ 混杂的题目，可以考虑使用图形简化分析，下面以两个数引入，再辅以例题加深理解
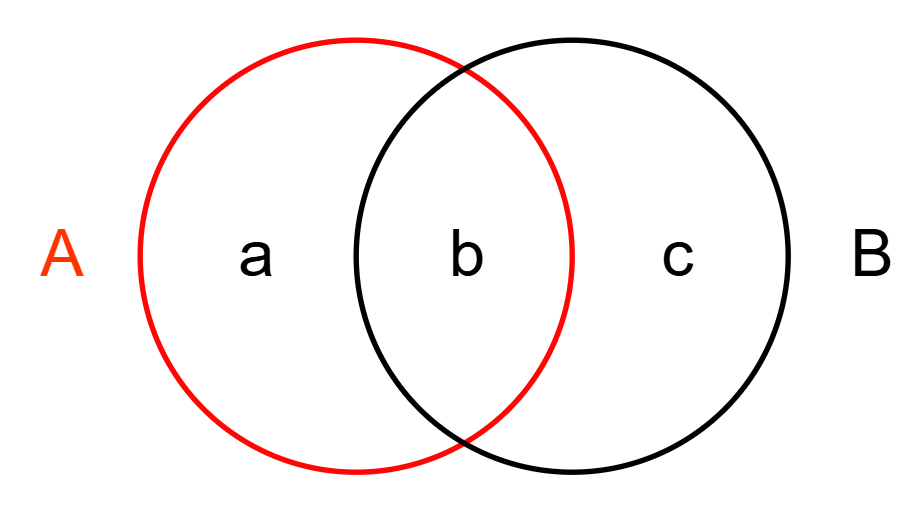
对于数 $A$ 和 $B$，由唯一分解定理有：

$$A=\prod_{i=1}^{k_1} (a_i^{x_i}),~B=\prod_{i=1}^{k_2}(b_i^{y_i})$$

图形化表示为：

以 $A$ 为例，$a$ 代表只在 $A$ 的唯一分解中出现的所有因子的乘积，$b$ 表示既在 $A$ 的唯一分解中出现也在 $B$ 的唯一分解中出现的所有因子的乘积
那么，显然， GCD(A, B) = b ， LCM(A, B) = a * b * c ，下面给出一个例题

# 2024 蓝桥杯省 B 宝石组合

# 题目大意

给你 $n$ 个数，$a_1,...,a_n$，你可以从中任选三个数 $(H_a,H_b,H_c)$，计算一个 $S$ 值

$$S = H_a H_b H_c \cdot \frac{\operatorname{LCM}(H_a, H_b, H_c)}{\operatorname{LCM}(H_a, H_b) \cdot\operatorname{LCM}(H_a, H_c) \operatorname{LCM}(H_b, H_c)}$$

你需要使得 $S$ 尽可大，请你找出 $S$ 最大的选数方案。如果存在多个方案 $S$ 值相同，优先选择按照 $H$ 值升序排列后字典序最小的方案

# 数据规模与约定

• 对 $30\%$ 的数据，$n \leq 100$，$H_i \leq 10^3$。
• 对 $60\%$ 的数据，$n \leq 2 \times 10^3$。
• 对全部的测试数据，保证 $3 \leq n \leq 10^5$，$1 \leq H_i \leq 10^5$。

# 题解

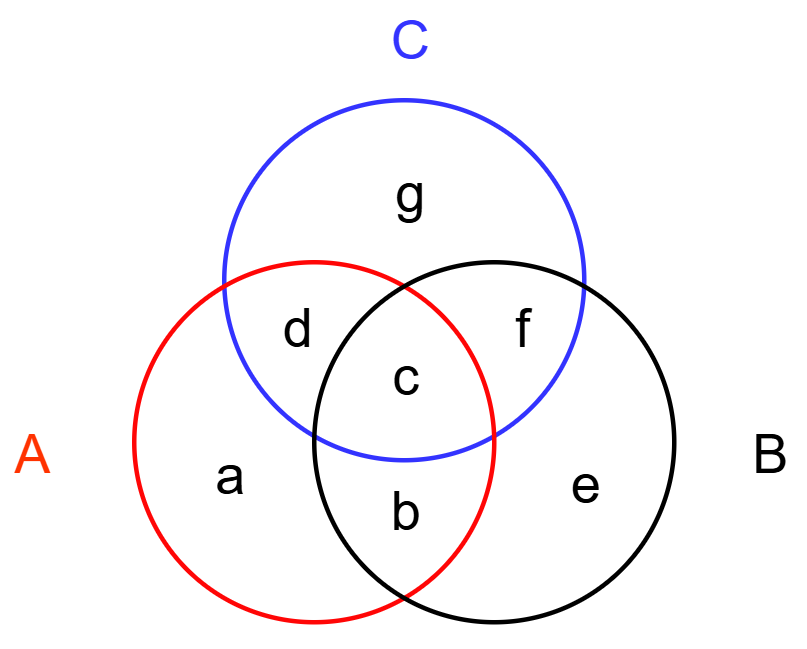
将三个数绘制如下图

那么，原式可以化为

$$S = (a·b·c·d) \times (b·c·f·e) \times (c·d·g·f) \times \frac{a·b·c·d·e·f·g}{(a·b·c·d·e·f) \times (b·c·e·f·d·g) \times (a·b·c·d·f·g)}$$

消元有，$S=c$，即代表，$S=GCD(A,B,C)$，也就是说，题目要找到三个数，满足 $GCD$ 最大