首页 程序设计 杂题集

# 填空题

# 1 握手问题

水

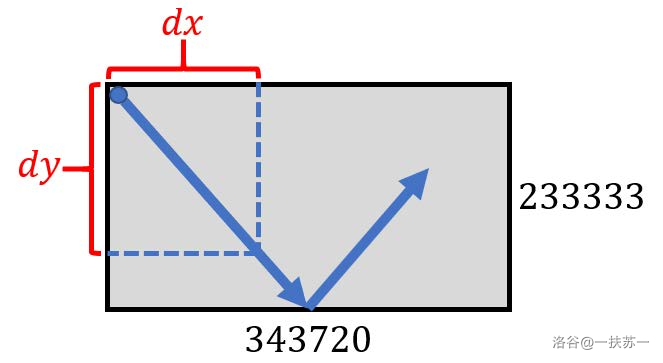
# 2 反弹问题


对于反弹问题，直接考虑较复杂，而将反弹过程展开，可以得到完整的若干个矩形拼起来。

C++
1
2
3
4
5
6
void solve () {
    int a = 343720, b = 233333;
    int m = 1059, n = 1768;

    printf("%.2lf", sqrt(a * a * m * m + b * b * n * n) * 2);
}

# 编程题

# 1 好数

# 题目大意

求 1→n1 \to n 中有多少个好数

# 题解

C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
bool judge(int n) {
    bool pd = 1;
    while (n != 0) {
        if ((n % 10) % 2 != (pd ? 1 : 0))
            return false;
        pd = !pd, n /= 10;
    }

    return true;
}

void solve () {
    int n, cnt = 0;
    cin >> n;
    for (int i = 1; i <= n; i++)
        if (judge(i))
            cnt++;
    cout << cnt << endl;
}

# 2 R 格式

# 题目大意

给定一个整数 nn 和一个浮点数 dd，你需要

  1. 将浮点数乘以 2n2^n
  2. 四舍五入到最接近的整数

# 数据范围

用 tt 表示将 dd 视为字符串时的长度。

  • 对于 50%50\% 的数据，保证 n≤10n \le 10，t≤15t \le 15
  • 对于全部的测试数据，保证 1≤n≤10001 \le n \le 1000，1≤t≤10241 \le t \le 1024，保证 dd 是小数，即包含小数点

# 题解

# 错解（高精乘 + 高精加)

C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
int n;
string d;

string add(string aa, string bb) {
    int la = aa.size(), lb = bb.size();
    vector<int> a, b, c;

    for (int i = la - 1; i >= 0; i--)
        a.push_back(aa[i] - '0');
    for (int i = lb - 1; i >= 0; i--)
        b.push_back(bb[i] - '0');

    int t = 0;
    for (int i = 0; i < max(la, lb); i++) {
        if (i < a.size())
            t += a[i];
        if (i < b.size())
            t += b[i];

        c.push_back(t % 10), t /= 10;
    }

    if (t)
        c.push_back(t);

    string res = "";
    for (int i = c.size() - 1; i >= 0; i--)
        res += to_string(c[i]);

    return res;
}

string mul(string aa, string bb) {
    int la = aa.size(), lb = bb.size();
    vector<int> a, b, c(la + lb, 0);

    for (int i = la - 1; i >= 0; i--)
        a.push_back(aa[i] - '0');
    for (int i = lb - 1; i >= 0; i--)
        b.push_back(bb[i] - '0');

    for (int i = 0; i < la; i++)
        for (int j = 0; j < lb; j++)
            c[i + j] = a[i] * b[j];

    int lc = c.size() - 1;
    
    for (int i = 0; i < lc; i++)
        if (c[i] > 9)
            c[i + 1] += c[i] / 10, c[i] %= 10;

    while (lc > 0 && c[lc] == 0)
        lc--;

    string res = "";

    for (int i = lc; i >= 0; i--)
        res += to_string(c[i]);

    return res;
}

void solve () {
    cin >> n >> d;
    string n2 = "1";
    while (n--)
        n2 = mul(n2, "2");

    int idx = d.find('.');

    int xsCnt = d.size() - d.find('.') - 1;
    // cout << xsCnt;

    string dd = d.substr(0, idx) + d.substr(idx + 1, xsCnt);

    string res = mul(n2, dd);
 
    string zs = res.substr(0, res.size() - xsCnt);

    // string sss = add("2", "1");
    // cout << sss << endl;
    if (res[res.size() - xsCnt] >= '5')
        cout << add(zs, "1");
    else
        cout << zs;
}

# 正解

对于 ×2n\times 2^n 的题目，我们可以考虑成不断 ×2\times 2，乘 nn 次即可，这样就可以把高精度 ×\times 高精度的题目改为高精度 ×\times 低精度了

C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
int n;
string d;

string mul(string aa, int b) {
    int la = aa.size();
    vector<int> a, c;
    for (int i = la - 1; i >= 0; i--)
        a.push_back(aa[i] - '0');

    int t = 0;

    for (int i = 0; i < la || t != 0; i++) {
        if (i < la)
            t += a[i] * b;
        c.push_back(t % 10), t /= 10;
    }

    while (!c.empty() && c.back() == 0)
        c.pop_back();
    
    string res = "";
    for (int i = c.size() - 1; i >= 0; i--)
        res += to_string(c[i]);
    return res;
}

void solve () {
    cin >> n >> d;
    int idx = d.find('.');
    int xsCnt = d.size() - idx - 1;

    string dd = d.erase(d.find('.'), 1);

    for (int i = 1; i <= n; i++)
        dd = mul(dd, 2);

    if (dd[dd.size() - xsCnt] < '5')
        cout << dd.substr(0, dd.size() - xsCnt);
    else {
        string res = "";
        string ss = dd.substr(0, dd.size() - xsCnt);
        reverse(ss.begin(), ss.end());

        int t = 1;
        for (int i = 0; i < ss.size() || t != 0; i++) {
            if (i < ss.size())
                t += ss[i] - '0';
            res += to_string(t % 10), t /= 10;
        }

        for (int i = res.size() - 1; i >= 0; i--)
            cout << res[i];
    }
}

# 3 宝石组合

# 题目大意

对于 nn 个数 a1,...,ana_1,...,a_n，找出 MAX(gcd(a[i], a[j], a[k]) 的最小字典序

# 数据范围

  • 1≤n≤1051 \le n \le 10^5
  • 1≤ai≤1051 \le a_i \le 10^5

# 题解