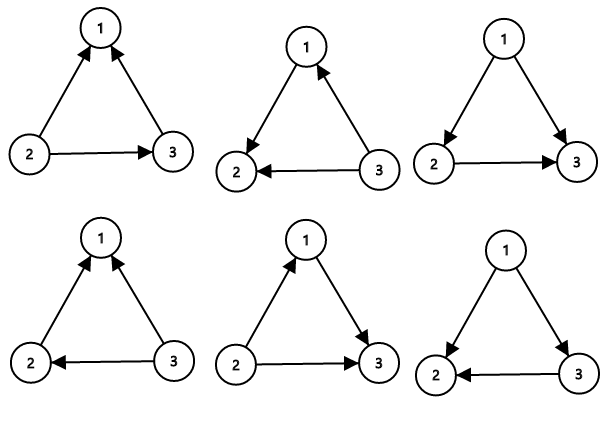
# 基环树是什么？

~~基环树其实是图~~
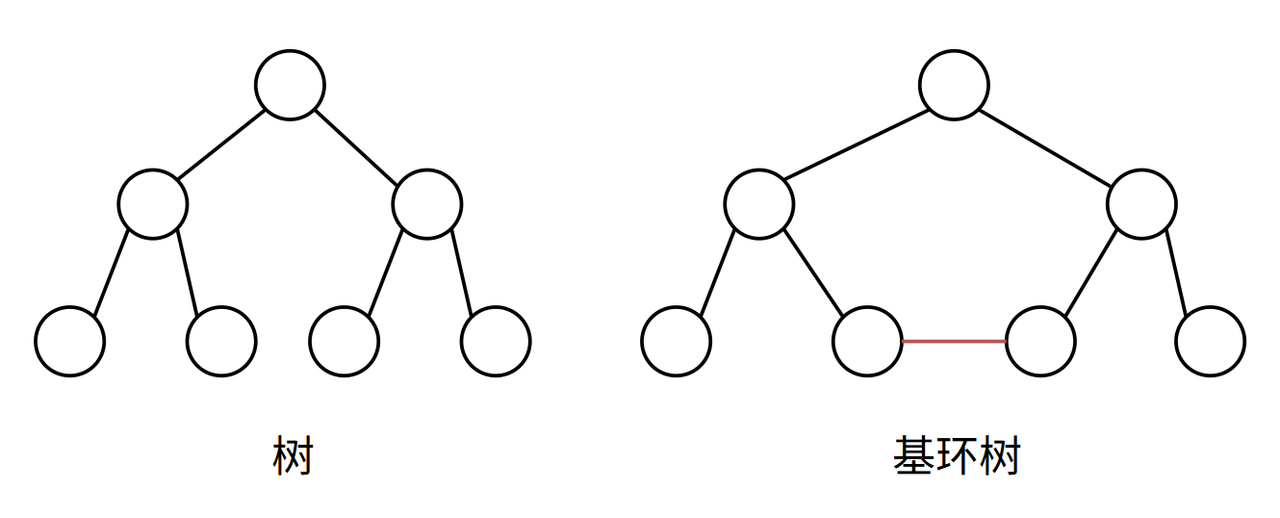
给一棵树加上一条边，那么树就会产生唯一的一个环，这样的图就叫基环树
如果是森林，那么可以是多个基环树

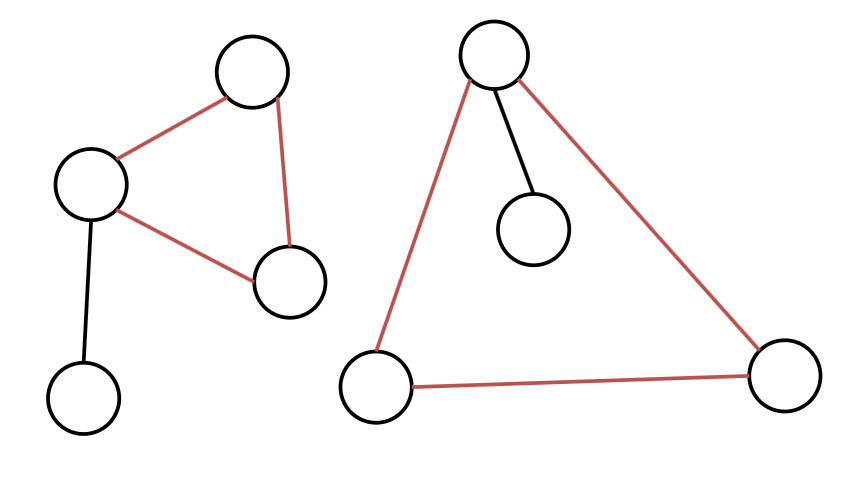
# 基环树森林

# 基环树的性格（bushi

内 / 外向基环树其实都是有向图

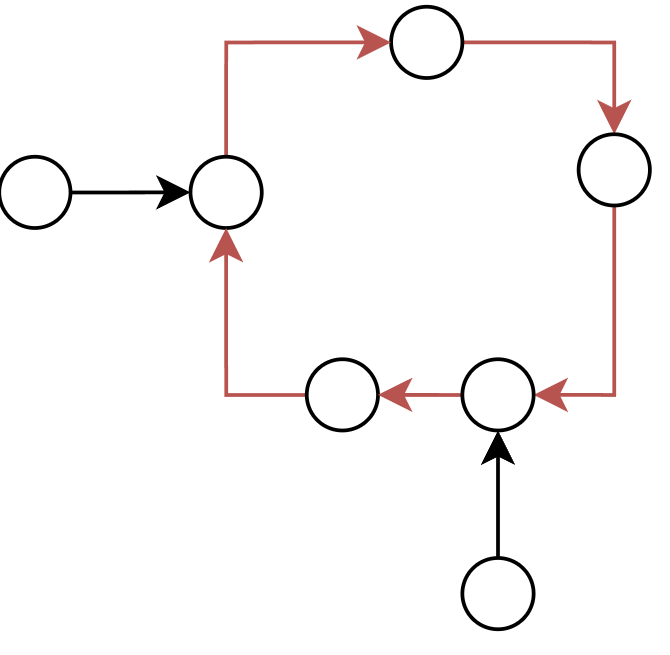
# 内向基环树

每个点的出度都只为 $1$ ，且环外点指向环内点

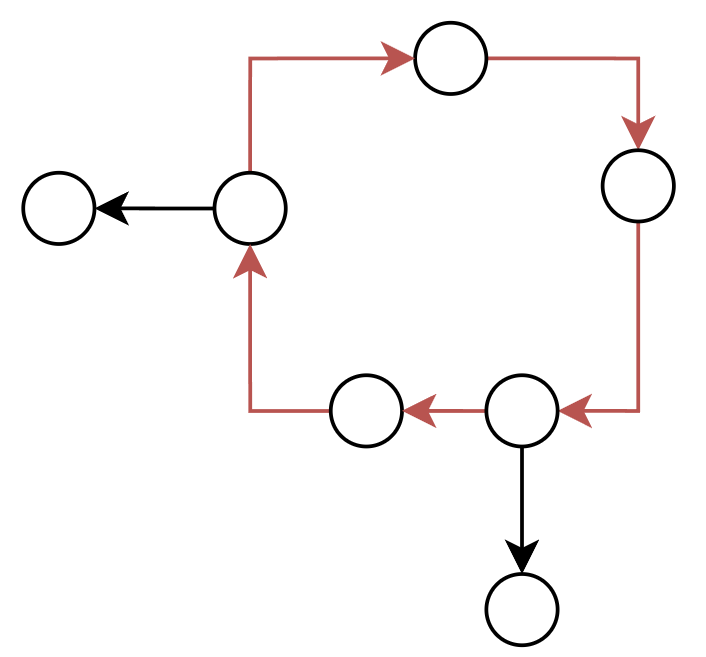
# 外向基环树

每个点的入度都只为 $1$ ，且环内点指向环外点

# 例题

# Directed Roads

# 题目大意

有 $n$ 个点和 $n$ 条边，第 $i$ 条边连接了 $i$ 点和 $a_i$ 点，每条边都需要指定一个方向，问有多少种指定方向的方案使得图中不出现环？
（此环非彼环，是可以沿着边一圈的环）

# 数据范围

$2 \le n \le 2·10^5$

# 样例

# 输入

1
2

3
2 3 1

# 输出

OUT

# 样例说明

# 题解

把点集分为环上的点和不在环上的点两部分考虑，假设第 $i$ 个环上有 $w_i$ 个点 z

不在环上的点，边的方向任意选，也就是 $2^{n - \sum{w_i}}$ 种方案

在环上的点，只有两种可能会构成环

1 \to 2 \to ... \to w_i \to 1

或

1 \leftarrow 2 \leftarrow ... \leftarrow w_i \leftarrow 1

，也就是，对于一个环而言，有

2^{w_i} - 2

种方案
共计：

(2^{n - \sum{w_i}})

(\prod{2^{w_i} - 2})

种方案
那么怎么求环数和环内点数呢？

C++

int depth[N];
int st[N];
vector<int> g[N];
vector<int> r;

void dfs(int u, int dep) {
    depth[u] = dep, st[u] = 1;

    for (auto &v : g[u]) {
        if (st[v] == 0)
            dfs(v, dep + 1);
        else if (st[v] == 1)
            r.push_back(depth[u] - depth[v] + 1);
    }

    st[u] = 2;
}

复杂度 $O(N+E)$ $O (N + E)$
- $N$ ：点数
- $E$ ：边数

总结一下就可以得到 $AC$ 代码哩

C++

int depth[N];
int st[N];
vector<int> g[N];
vector<int> r;

int n;

int qmi(int x, int y) {
    int res = 1;
    while (y) {
        if (y & 1)
            res = res * x % MOD;
        x = x * x % MOD, y >>= 1;
    }

    return res % MOD;
}

void dfs(int u, int dep) {
    depth[u] = dep, st[u] = 1;

    for (auto &v : g[u]) {
        if (st[v] == 0)
            dfs(v, dep + 1);
        else if (st[v] == 1)
            r.push_back(depth[u] - depth[v] + 1);
    }

    st[u] = 2;
}

void solve () {
    cin >> n;
    for (int i = 1, x; i <= n; i++)
        cin >> x, g[i].push_back(x);

    for (int i = 1; i <= n; i++)
        if (depth[i] == 0)
            dfs(i, 1);

    int sum = 0, res = 1;
    for (int t : r)
        sum += t, res = res * (qmi(2, t) - 2 + MOD) % MOD;

    cout << res * qmi(2, n - sum) % MOD << endl;
}

图论基环树环