首页 程序设计 数据结构

参考连接传送门

# 什么是树状数组？

结构为树形结构的数组，与二叉树结构有些类似

  • 二叉树结构示意图：
  • 树状数组结构示意图：

# 可以解决的问题

可以解决大部分区间修改以及查询问题

  • 单点修改，单点查询
  • 区间修改，单点查询
  • 区间查询，区间修改

# 相较线段树，树状数组的优缺点

  • 优点：修改和查询操作复杂度于线段树一样都是 logNlogN，但是常数比线段树小，并且实现简单
  • 缺点：扩展性弱，线段树能解决的问题，树状数组不一定能解决

# 前置知识 - lowbit (x) 运算

如何计算一个非负整数 nn 在二进制下的最低为 11 及其后面的 00 构成的数

例：44=(101100)244 = (101100)_2，lowbit(44)=(100)2=4lowbit(44) = (100)_2 = 4

lowbit(x) = x & (-x)

# 问题引入

# 题目背景

给出一个长度为 nn 的数组，完成以下两种操作

  • 将第 xx 个数加上 kk
  • 输出 ∑i=xyai,(1≤x≤y≤n)\sum\limits_{i=x}^y a_i,(1 \le x \le y \le n)

# 暴力做法

加完之后再扫一遍 ax→aya_x \to a_y

# 树状数组优化


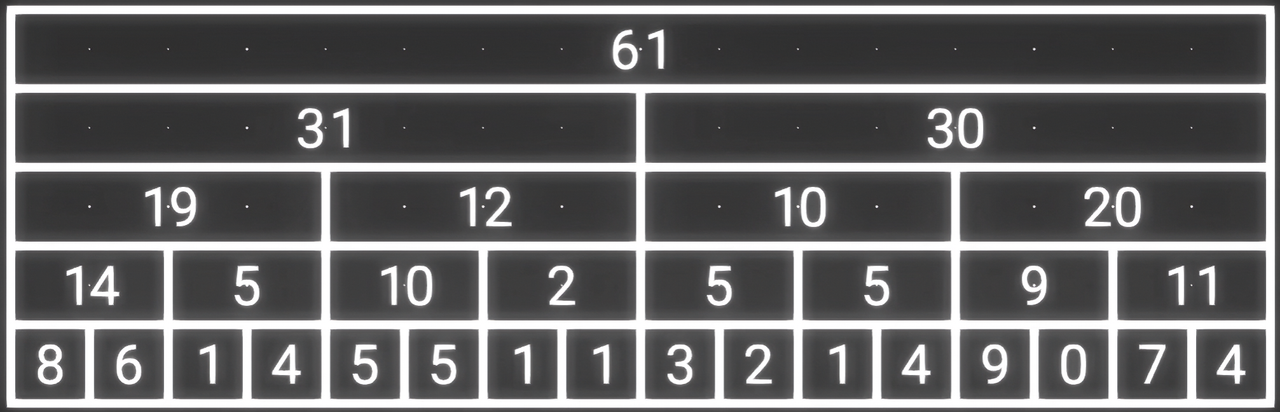
不断求和，这样算前 ii 个的和就可以用所求出来的子段和来表示
例如想求前 77 个，则可以用 19 + 10 + 1 来表示

观察有，每层的偶数位置的字段，都不会被用到，可以直接删掉

删除后，恰好剩下的数是 nn 个・

  • 计算和时，只需要找到对应区间相加
  • 修改值时，只要在竖直方向修改对应区间即可

树状数组巧妙地利用了二进制

# 树状数组的查询

例如求前 11,(1011)211,(1011)_2 位的和，可以这样求：
sum=((0000)2,(1000)2]+((1000)2,(1010)2]+((1010)2,(1011)2]sum=((0000)_2, (1000)_2] + ((1000)_2, (1010)_2] + ((1010)_2, (1011)_2]
不断去掉二进制的最后一个一，求区间和

# 树状数组的更新

# 优化代码

c++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <bits/stdc++.h>
#define int long long
#define endl '\n'

using namespace std;

typedef pair<int, int> PII;
const int N = 5e5 + 10;
int dx[] = {0, 0, 0, 1, -1, 1, 1, -1, -1};
int dy[] = {0, 1, -1, 0, 0, 1, -1, 1, -1};

int n, q, ask, x, y, a[N];

int lowbit(int n) {
    return (n & -n);
}

void add(int p, int x) {
    while (p <= n)
        a[p] += x, p += lowbit(p);
}

int count(int p) {
    int res = 0;
    while (p)
        res += a[p], p -= lowbit(p);
    return res;
}

void solve () {
    cin >> n >> q;
    for (int i = 1, x; i <= n; i++)
        cin >> x, add(i, x);

    while (q--) {
        cin >> ask >> x >> y;

        if (ask == 1)
            add(x, y);
        else
            cout << count(y) - count(x - 1) << endl;
    }
}

signed main () {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);

    int _ = 1;
    //cin >> _;

    while(_--)
       solve();

    return 0;
}