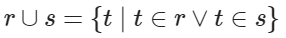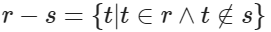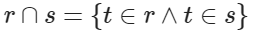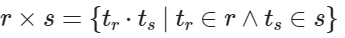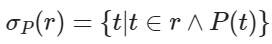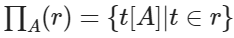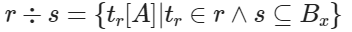首页 学习学习我爱学习 数据库

# 一些前置知识

  • 与：∧\wedge
  • 或：∨\vee
  • 非：⌝\urcorner

# 传统的集合运算

# 并

关系 rr 和关系 ss 的并记作

# 差

关系 rr 和关系 ss 的差记作：

# 交

关系 rr 和关系 ss 的交记作：

# 笛卡尔积

两个分别为 nn 目和 mm 目的关系 rr 和 ss 的笛卡尔积是一个 n+mn+m 目元组的集合。若关系 rr 有 krk_r 个元组，关系 ss 有 ksk_s 个元组，则关系 rr 和关系 ss 的笛卡尔积有 kr∗ksk_r * k_s 个元组，记作：

# 专门的关系运算

# 选择

选择操作是在关系 rr 中查找满足给定谓词（选择条件）的所有元组，记作：

# 投影

关系是一张二维表，对它的操作可以从水平（行）的角度进行，即选择操作；也可以从纵向（列）的角度进行，即投影操作
关系 rr 上的投影是从 rr 中选择出若干属性列组成新的关系，记作：

# 连接

连接也称 θ\theta 连接，假设连接条件为谓词 θ\theta，记为 AopBA~op~B，其中 A,BA,B 分别表示关系 rr 和关系 ss 中的属性个数相等且可比的连接属性集，opop 为比较运算符，则 θ\theta 连接是从两个关系的笛卡尔积中，选取连接属性间满足谓词 θ\theta 的所有元
组，记作：r∏θs={tr⋅ts∣tr∈r∧ts∈s∧(r.Aops.B)}r \prod_\theta s = \{ t_r · t_s ~ | ~ t_r \in r \wedge t_s \in s \wedge (r.A ~ op ~ s.B) \}
θ\theta 连接运算就是从关系 rr 到关系 ss 的笛卡尔积 r×sr \times s 中，选取 rr 关系在 AA 属性集上的值与 ss 关系在 BB 属性集上的值满足连接谓词 θ\theta 的所有元组，即：r⋈θs=σθ(r×s)r \bowtie_\theta s = \sigma_\theta(r \times s)

# 自然连接

自然连接是一种特殊的等值连接，它要求两个参与连接的关系 r(U)r(U) 和 s(V)s(V) 具有公共的属性集，即 U∩V≠∅U \cap V \neq \emptyset，并在这个公共属性集上进行等值连接；同时，还要求将连接结果中的重复属性列去掉，即在公共属性集中的列只保留一次。
记 U∩V={A1,...,Ak}U \cap V = \{A_1,...,A_k\}，则自然连接可记作：r⋈s={(tr⋅ts)[U∪V]∣tr∈r∧ts∈s∧(r.A1=s.A1∧...∧r.Ak=s.Ak)=∏U∪V(σr.A1=s.A1∧...∧r.Ak=s.Ak(r×s))r \Join s = \{ (t_r · t_s)[U \cup V] ~ | ~ t_r \in r \wedge t_s \in s \wedge (r.A_1 = s.A_1 \wedge ... \wedge r.A_k = s.A_k)=\prod_{U \cup V}(\sigma_{r.A_1 = s.A_1 \wedge ... \wedge r.A_k = s.A_k}(r \times s))
自然连接满足结合律。如果公共属性集为空，则自然连接的结果就是笛卡尔积

# 除运算

为了叙述方便，先给出象集的概念

# 象集

给定一个关系 r(A,B)r(A,B)，A,BA,B 为属性集。∀t∈r\forall t \in r，记 t[A]=xt[A]=x，则在关系 rr 中属性集 AA 的某个取值 xx 的象集定义为：Bx={t[B]∣t∈r,t[A]=x}B_x = \{ t[B] ~ | ~ t \in r, t[A]=x \}，表示关系 rr 中属性集 AA 上取值为 xx 的所有元组在属性集 BB 上的投影

# 除运算的定义

设关系 r(A,B)r(A,B) 和 S(B)S(B)，A,BA,B 是属性集，将关系 rr 和关系 ss 之间的除运算记作 r÷sr \div s，除运算的结果还是一个关系，它是关系 rr 中满足下列条件的元组 trt_r 在属性集 AA 上的投影：∀tr∈r\forall t_r \in r，记 x=tr[A]x = t_r[A]，要求关系 rr 中属性集 AA 上取值 xx 的象集 BxB_x 包含关系 ss，记作：