首页 程序设计 数据结构

# 概念

并查集是一种用于管理元素所属集合的数据结构，实现为一个森林，其中每棵树表示一个集合，树中的节点表示对应集合中的元素
并查集用来处理一些不相交的集合合并的问题，支持两种基本操作

  • 合并（ UnionUnion ）：合并两个元素所属集合（合并对应的树）
  • 查询（ FindFind ）：查询某个元素所属集合（查询对应的树的根节点），这可以用于判断两个元素是否属于同一集合

# 基本操作

# 初始化

每个数 ii 的 fif_i 都等于本身

c++
1
2
3
void init() {
	for (int i =1; i <= n; i++)    f[i] = i;
}

# 查询

c++
1
2
3
int find(int u) {
	return (u == f[u] ? f[u] : f[u] = dfs(f[u]));
}

# 合并

c++
1
2
3
4
5
void union(int a, int b) {
	int fa = find(a), fb = find(fb);

	f[fa] = fb;
}

# 例题传送门 1

# 题目描述

有 nn 个同学（编号为 11 到 nn）正在玩一个信息传递的游戏。在游戏里每人都有一个固定的信息传递对象，其中，编号为 ii 的同学的信息传递对象是编号为 TiT_i 的同学。游戏开始时，每人都只知道自己的生日。之后每一轮中，所有人会同时将自己当前所知的生日信息告诉各自的信息传递对象（注意：可能有人可以从若干人那里获取信息，但是每人只会把信息告诉一个人，即自己的信息传递对象）。当有人从别人口中得知自己的生日时，游戏结束。请问该游戏一共可以进行几轮？
对于 100%100\% 的数据，n≤2×105n\le 2\times 10^5

# 思路

并查集大王，但是不用路径压缩的并查集，用普通并查集，通过并查集里加个 cntcnt 变量来模拟一轮游戏向上找的过程

c++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
int n, f[N], a[N];

int find(int u, int& cnt) {
    cnt++;

    if (u == f[u])
        return u;
    else
        return find(f[u], cnt);
}

void solve () {
    int minn = 0x3f3f3f3f;

    cin >> n;
    for (int i = 1; i <= n; i++)
        f[i] = i;

    for (int i = 1, t; i <= n; i++) {
        int cnt = 0;
        cin >> t;
        
        if (find(t, cnt) == i)
            minn = min(minn, cnt);
        else
            f[i] = t;
    }

    cout << minn << endl;
}

# 例题传送门 2

# 题目描述

动物王国中有三类动物 A,B,CA,B,C 这三类动物的食物链构成了有趣的环形。AA 吃 BB，BB 吃 CC，CC 吃 AA。现在一共有 NN 个动物，以 1∼N1 \sim N 编号。每个动物都是 A,B,CA,B,C 中的一种，但是我们并不知道它到底是哪一种
有人用两种说法对这 NN 个动物所构成的食物链关系进行描述：

  • 第一种说法是 1 X Y ，表示 XX 和 YY 是同类
  • 第二种说法是 2 X Y ，表示 XX 吃 YY

此人对 NN 个动物，用上述两种说法，一句接一句地说出 KK 句话，这 KK 句话有的是真的，有的是假的。当一句话满足下列三条之一时，这句话就是假话，否则就是真话

  • 当前的话与前面的某些真的话冲突，就是假话
  • 当前的话中 XX 或 YY 比 NN 大，就是假话
  • 当前的话表示 XX 吃 XX，就是假话

你的任务是根据给定的 NN 和 KK 句话，输出假话的总数

# 数据范围

对于全部数据，1≤N≤5×1041\le N\le 5 \times 10^4，1≤K≤1051\le K \le 10^5

# 思路

利用并查集存额外信息，此处利用并查集存了某个结点到根节点的距离

# 同集合确定关系

利用环状相食的关系，可以使用模 + 任意两点到根点的距离来确定同一集合中，不同点的相互关系

  • d[x] % 3 == d[y] % 3 ：xx 和 yy 是同类
    • (d[x] - d[y]) % 3 == 0
  • d[x] % 3 - 1 == d[y] % 3 ：xx 吃 yy
    • (d[x] - x - d[y]) % 3 == 0

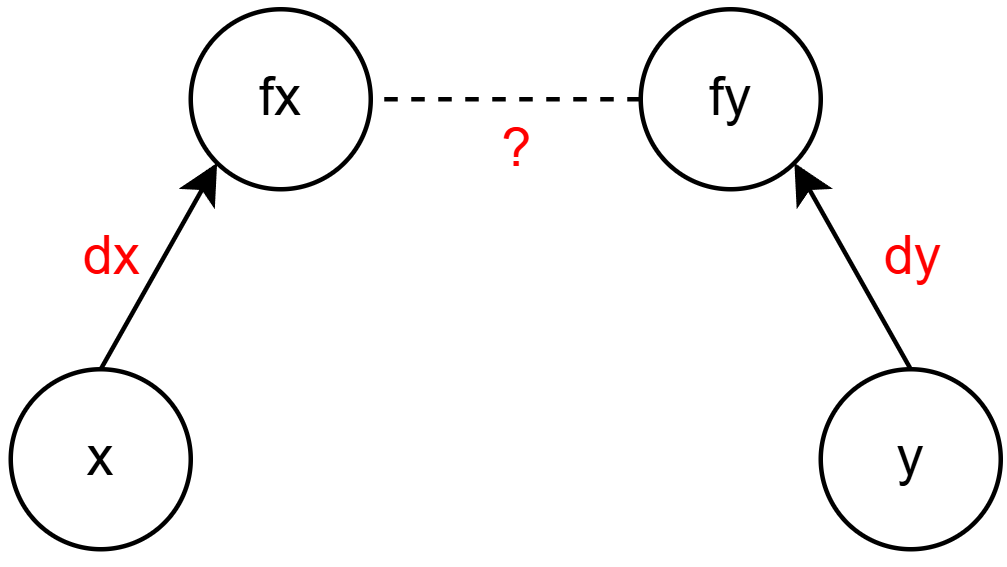
# 不同集合进行合并

  • 若 xx 和 yy 是同类，则有 (d[x] + ? - d[y]) % 3 == 0
    • 即为 ? = d[y] - d[x]
  • 若 xx 吃 yy，则有 (d[x] + ? - 1 - d[y]) % 3 == 0
    • 即为 ? = d[y] + 1 - d[x]

# 代码

C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <bits/stdc++.h>
#define int long long
#define endl '\n'

using namespace std;

const int N = 5e4 + 10;
int n, k, t, x, y, f[N], d[N];

int find(int x) {
    if (x != f[x]) {
        int t = find(f[x]);
        d[x] += d[f[x]], f[x] = t;
    }

    return f[x];
}

void solve() {
    cin >> n >> k;
    for (int i = 1; i <= n; i++)    f[i] = i;

    int cnt = 0;
    while (k--) {
        cin >> t >> x >> y;

        if (x > n || y > n) {
            cnt++;
            continue;
        }

        int fx = find(x), fy = find(y);

        if (t == 1) {
            if (fx == fy && (d[x] - d[y]) % 3)  cnt++;
            else if (fx != fy)  f[fx] = fy, d[fx] = d[y] - d[x];
        }
        else {
            if (fx == fy && (d[x] - d[y] - 1) % 3)  cnt++;
            else if (fx != fy)  f[fx] = fy, d[fx] = 1 + d[y] - d[x];
        }
    }
    cout << cnt << endl;
    return;
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);

    int t = 1;
    while (t--) solve();

    return 0;
}