# 运输问题模型

已知有 $m$ 个产地 $A_i,i=1,2,...,m$，供应某物资的供应量分别为 $a_i,i=1,2,...,m$；有 $n$ 个销地 $B_j,j=1,2,...,n$，其物资需求量分别为 $b_j,j=1,2,...,n$
从 $A_i$ 到 $B_j$ 运输单位物资的运价（单价）为 $c_{ij}$，求总费用最小的运输方案。

设 $x_{ij}$ 表示从 $A_i$ 到 $B_j$ 的运量，在产销平衡的条件下，运输问题的数学模型为：

$$min Z = \sum\limits^{m}_{i=1} \sum\limits^{n}_{j=1} c_{ij}x_{ij},~ \begin{cases} \sum\limits^{n}_{j=1} x_{ij}=a_i,i=1,2,...,m\\ \sum\limits^{m}_{i=1}x_{ij}=b_j,j=1,2,...,n\\ x_{ij} \ge 0, i=1,2,...,m;~j=1,2,...,n \end{cases}$$

# 运输问题特点

• 决策变量数：$mn$ 个
• 约束方程数：$m+n$ 个
• 由产销平衡得：$\sum\limits^{m}_{i=1}a_i=\sum\limits^{m}_{i=1}(\sum\limits^{n}_{j=1}x_{ij})=\sum\limits^{n}_{j=1}(\sum\limits^{m}_{i=1}x_{ij})=\sum\limits^{n}_{j=1}b_j$
  • 独立约束：最多有 $m+n-1$ 个独立约束

# 表上作业法

1. 求初始基本可行解（西北角法、最小元素法、伏格尔法）
2. 求检验数并判断（闭回路法、位势法）
3. 调整变量（闭回路法）
4. 重复步骤二、三，直到求得最优解

# 求初始基本可行解

# 西北角法

# 求解思路

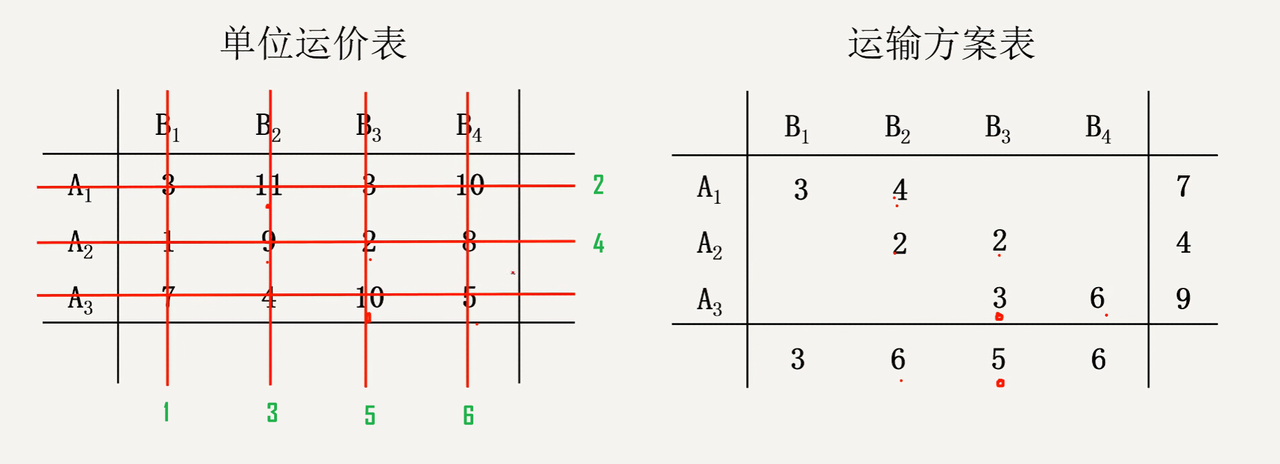
从单位运价表未被直线覆盖的西北角（左上角）位置开始标识即便，依次进行，直到找到 $m+n-1$ 个基变量为止

1. 在单位运价表中选择未被直线覆盖的左上角位置作为基变量
2. 对比基变量行、列，选择最小值作为基变量取值（是在运输方案表中填值，填的值与单位运价表的内容无关）
3. 用直线划去满足需求的行 / 列
   

# 缺陷

注意到，西北角法在填值的时候，并没有考虑到单位运价，只是将运输方案安排好了，所以有可能得到的运输方案会使得运价偏大。

# 最小元素法

# 求解思路

求单位运价表未被直线覆盖的最小运价位置开始标识变量，依次进行，知道找到 $m+n-1$ 个变量为止
步骤与西北角法相似，只是找位置的时候是用未被直线覆盖的最小运价位置，其余一模一样。

# 缺陷

在最开始时，为了节省某一处的费用，导致其他地方花费开支大。

# 伏格尔法

# 求解思路

寻找单位运价表 == 最小运价与次小运价差额最大的行 / 列 ==，从该行 / 列的最小运价位置开始标识基变量，依次进行，直到找到 $m+n-1$ 个基变量为止。
步骤与西北角法相似，只是找位置的时候选取方式不同，其余一模一样。

# 三种方法的比较

三种方法的总运价从上往下逐步递减。

# 求检验数并判断

# 闭回路法

# 原理

运输方案表中，任何一个非基变量都能和若干个基变量构成唯一一个闭回路

# 步骤

1. 从空格出发，水平 / 垂直画直线，遇到数字可前进 / 转 $90°$ (只能在有数字的地方转向)
2. 假设空格处增加一个运量，则相应调整闭回路顶点的运量
3. 计算调整运量后增加的运价，即为该空格处检验数
4. 目标函数求最小（大）值，所有检验数 $\ge 0~(\le 0)$，判断是否达到最优解

# 位势法

# 原理

对偶理论：$u_i+v_j=c_{ij},~\lambda_{ij}=c_{ij}-u_i-v_j$

# 步骤

1. 先在检验数表中，写入基变量对应的单位运价
2. 根据 $u_i+v_j=c_{ij}$，任令一个 $u_i$ 或 $v_j$ 等于零，解方程组
3. 再根据 $\lambda_{ij}=c_{ij}-u_i-v_j$，求出剩下的非基变量的检验数
4. 目标函数求最小（大）值，所有检验数 $\ge 0~(\le 0)$，判断是否达到最优解

# 调整变量

1. 选择检验数最小的非基变量作为进变量
2. 以进基变量作为起始点，在运输方案表上构建闭回路。选择闭回路上运量最小的基变量作为出变量
3. 对于出变量，在闭回路上调整至 $0$
4. 继续判断是否为最优解