# 对偶理论

• 对称性：对偶问题的对偶是原问题
• 弱对偶性：若 $\overline{X}$ 是原问题（特指 $max$ ）的可行解，$\overline{Y}$ 是对偶问题（特指 $min$ ）的可行解，则 $C \overline{X} \le \overline{Y}b$
• 无界性：若原问题（对偶问题）为无界解，则其对偶问题（原问题）无可行解
  • 原问题无界解 $\Rightarrow$ 对偶问题无可行解 或 对偶问题无界解 $\Rightarrow$ 原问题无可行解

$$\begin{cases} \text{对偶问题无可行解}\\ \\ \text{原问题有可行解} \end{cases} \Rightarrow \text{原问题无界解}$$

$$\begin{cases} \text{原问题无可行解}\\ \\ \text{对偶问题有可行解} \end{cases} \Rightarrow \text{对偶问题无界解}$$

• 最优性：设 $\hat{X}$ 是原问题的可行解，$\hat{Y}$ 是对偶问题的可行解，当 $C \hat{X} = \hat{Y} b$ 时，$\hat{X},~\hat{Y}$ 是最优解
• 对偶定理：若原问题有最优解，则对偶问题也有最优解，且目标函数值相等
• 互补松弛性：设 $\hat{X},~\hat{Y}$ 分别是原问题和对偶问题的可行解，$X_S,~Y_S$ 分别是其松弛变量的可行解，则 $\hat{X}$ 和 ${\hat{Y}}$ 是最优解 $\Longleftrightarrow$ $Y_S\hat{X}=0,~\hat{Y}X_S=0$

# 对偶单纯形法

单纯形表中检验数的绝对值对应其对偶问题的一组基本解

• 第 $j$ 个决策变量 $x_j$ 的检验数的绝对值对应对偶问题的第 $j$ 个松弛变量 $y_{s_j}$ 的解
• 第 $i$ 个松弛变量 $x_{s+i}$ 的检验数的绝对值对应对偶问题第 $i$ 个对偶变量 $y_i$ 的解

# 求解方法

1. 求出满足最优检验的基本解（即对偶问题的基可行解），建立初始单纯形表
2. 判断基本解是否满足非负约束，若满足则得到最优解，结束计算；否则进行下一步
3. 基变量（先确定出基变量，再确定进基变量），构建新的单纯形表进行迭代
4. 重复步骤二、三，直到得出最优解 / 无最优解

# 例题

用对偶单纯形法求解下列线性规划：

$$\min \omega = 2x_1 + 3x_2 + 4x_3,~ \begin{cases} x_1+2x_2+x_3\ge3 \\ 2x_1-x_2+3x_3\ge4\\ x_1,x_2,x_3\ge0 \end{cases}$$

# 对偶单纯形法优点

1. 初始解可以是非可行解，当检验数都非正时（目标函数为最小值则检验数都非负），就可以进行基变换，不需要添加人工变量
2. 当变量多于约束条件时，用对偶单纯形法可减少计算量
3. 在灵敏度分析及求解整数规划的割平面法中，有时需要用到对偶单纯形法

# 互补松弛性

# 前置证明

# 概念

# 题目

# 灵敏度分析

问：$a_{ij},~b_i,~c_j$ 系数中有一个或几个变化时，原线性规划最优解会怎么变化？
判断方法：把发生变化的系数经过一定计算代入原最终表中，进行检查和分析

# 价值系数的灵敏度分析

$c_j$ 发生变化，检验数 $\sigma_j$ 发生变化

• $c_j$ 对应非基变量，重新计算 $c_j$ 对应的检验数
• $c_j$ 对应基变量，重新计算所有非基变量的检验数

# 资源限量的灵敏度分析

若资源中某系数 $b_r$ 发生变化，即 $b_r^{'}=b_r+\Delta b$
则原问题最优解相应变化为：
$X_B^{'}=B^{-1}(b+\Delta b) = B^{-1}b+B^{-1}\Delta b$
$=B^{-1}b+B^{-1}[0,...,\Delta b_R,...,0]^\mathrm T$

# 技术系数的灵敏度分析

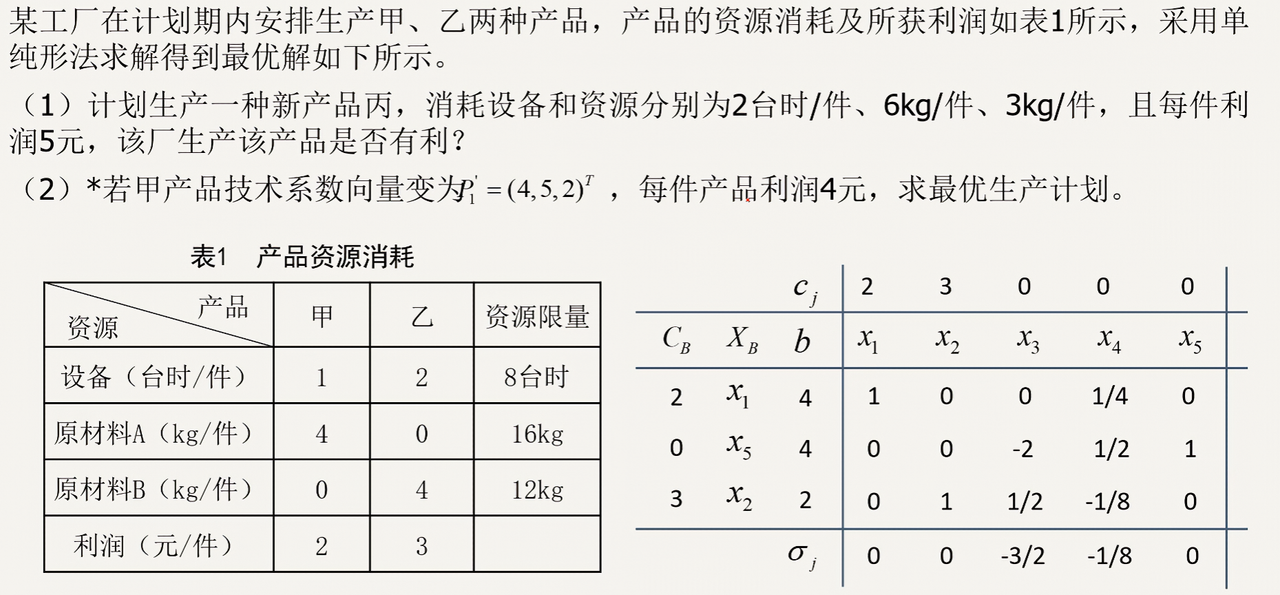
# 第一问

# 第二问